Студент: Фейденгеймер Артемис Витальевич

Группа: БЭАД-243

Вариант: 2330

Математический анализ II. Лабораторная работа¶

Правила:

Запрещено изменять функции! В тех задачах, где Вам дана функция в коде проверяться будет только код, написанный внутри этой данной функции. Также запрещено изменять значения переменных, которые определены кодом в некоторых заданиях.
Все считаем и выполняем с помощью кода. (Где необходимо: не забываем пояснять текстом).

Перед отправкой обязательно перезапустите ядро и скомпилируйте весь ноутбук заново!

Содержание работы¶

1. Ряды Фурье

v Задача 1 (1 балл)
v Задача 2 (2 балла)
? Задача 3 (2 балла)
v Задача 4 (2 балла)

2. Фильтрация звука с помощью DFT

v Задача 5 (1 балл)
v Задача 6 (3 балла)
v Задача 7 (3 балла)
v Задача 8 (4 балла)
v Задача 9 (1 балл)
v Задача 10 (4 балла)
v Задача 11 (5 баллов)
v Задача 12 (6 баллов)

3. Численное моделирование освещённости с использованием кратных интегралов

v Задача 13 (4 балла)
v Задача 14 (5 баллов)
v Задача 15 (5 баллов)
v Задача 16 (3 балла)
Задача 17 (8 баллов)

4. Scale-Invariant Feature Transform

v Задача 18 (2 балла)
Задача 19 (1 балл)
Задача 20 (8 баллов)
Задача 21 (2 балла)
Задача 22 (1 балл)
Задача 23 (11 баллов)

43/73

Необходимые библиотеки¶

# если не устанавливали
%pip install --upgrade pip
!pip install numpy
!pip install sympy
!pip install scipy
!pip install matplotlib
!pip install ipywidgets
!pip install soundfile
!pip install pandas
!pip install seaborn
!pip install opencv-python
!pip install scikit-learn

Fetching long content....

import math
import numpy as np
import sympy as sp
from numpy import pi as Pi_, cos as Cos
import scipy
import scipy.signal as signal
import scipy.signal as scsig
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.colors import LogNorm
from ipywidgets import interact, Output
from IPython.display import *
import soundfile as sf
import math
import pandas as pd
import datetime as dt
import seaborn as sns
# import cv2
from typing import Iterable, Tuple, Optional
from dataclasses import dataclass
from lab_utils import to_gray_float32, imshow, draw_keypoints, match_descriptors, show_matches # проверьте, что в проекте есть файл lab_utils.py
from sklearn.metrics import mean_absolute_error, mean_absolute_percentage_error
%matplotlib inline

Часть 1. Ряды Фурье¶

Ряд Фурьe — представление функции $f$ с периодом $T$ в виде ряда

f(x) \sim \frac{a_0}{2} + \sum_{n=1}^{\infty} \left( a_n \cos\left(\frac{2\pi n}{T} x\right) + b_n \sin\left(\frac{2\pi n}{T} x\right) \right) \tag{1} = S(x)

где коэффициенты $a_0$ , $a_n$ , и $b_n$ вычисляются следующим образом:

a_0 = \frac{1}{l} \int_{-l}^{l} f(x) \, dx \tag{2}

a_n = \frac{1}{l} \int_{-l}^{l} f(x) \cos\left(\frac{\pi n}{l} x\right) \, dx \tag{3}

b_n = \frac{1}{l} \int_{-l}^{l} f(x) \sin\left(\frac{\pi n}{l} x\right) \, dx \tag{4}

Где $T = 2l$

Для дальнейших вычислений нам понадобятся следующие знания:

Функция $f(х)$ называется кусочно-непрерывной на отрезке $[а, b]$ , если она непрерывна во всех точках этого отрезка, кроме, может быть, конечного числа точек, в которых она терпит разрывы первого рода (имеет конечные односторонние пределы).
Кусочно-непрерывная на отрезке $[а, b]$ функция $f(x)$ называется кусочно-гладкой, если она имеет непрерывную производную во всех точках этого отрезка, кроме, может быть, конечного числа точек, в которых производная функции терпит разрывы первого рода.
Основная теорема о сходимости тригонометрических рядов Фурье может быть сформулирована следующим образом. Пусть $f(х)$ кусочно-гладкая на отрезке $[-l, l]$ функция. Тогда тригонометрический ряд Фурье $(1)$ , коэффициенты которого вычисляются по формулам $(2)-(4)$ , сходится в каждой точке этого отрезка. Если $S(x)$ - сумма тригонометрического ряда Фурье функции $f(x)$ , то

$S(x) = f(x)$ во всех точках непрерывности функции $f(x)$ , $х ∈ (-l,l)$ ;
$S(x) = \frac{1}{2} (f(x - 0) + f(x + 0))$ во всех точках разрыва функции;
$S(-l) = S(l) = \frac{1}{2}(f(-l + 0) + f(l - 0))$ (здесь $f(x - 0)$ - предел слева, а $f(x + 0)$ - предел справа функции $f(x)$ в точке $x$ ).

Можем взглянуть на результаты добавления членов ряда Фурье при аппроксимации разрывной кусочно-постоянной функции.

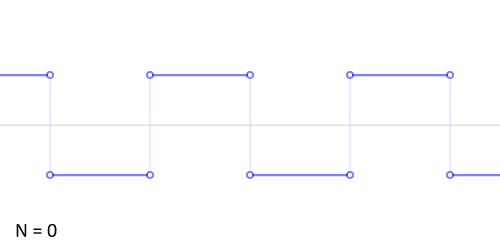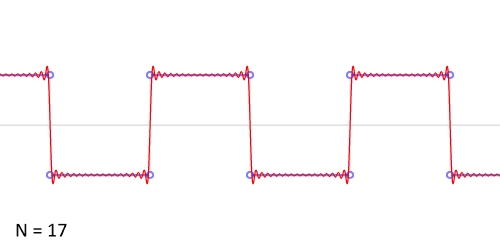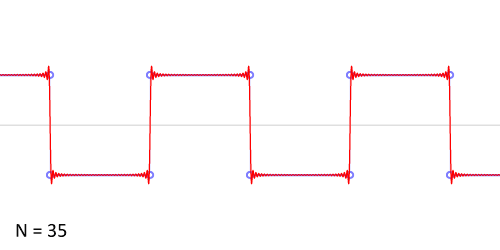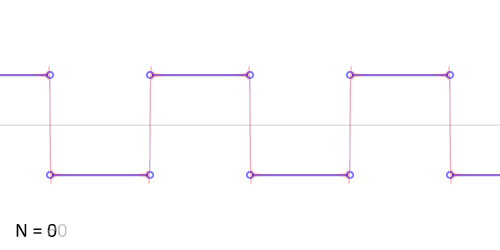
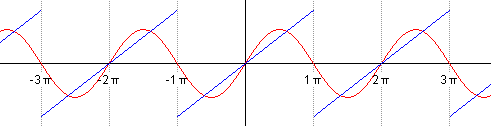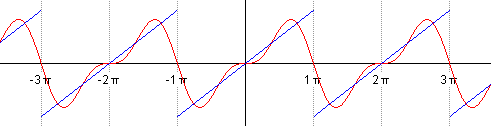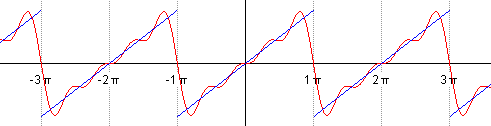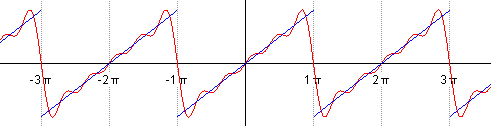
Авторство: Lucas Vieira. Собственная работа, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=468472

Авторство: Lucas Vieira. Собственная работа, Общественное достояние, https://commons.wikimedia.org/w/index.php?curid=1213511

Ряды Фурье имеют широкий спектр применений в различных областях, включая анализ сигналов, обработку изображений, решение дифференциальных уравнений, а также в физике, инженерии и многих других дисциплинах. Они позволяют удобно работать с периодическими явлениями, помогая выявить гармонические компоненты в сигнале и понять их влияние.

В качестве примера давайте разложим функцию $f(x) = x + 1$ в ряд Фурье на промежутке $[-\pi, \pi]$ , а также построим график функции $f(x) = x + 1$ соседних периодах и график частичной суммы ряда $S_2(x)$ на этих же периодах.

В данной задаче период разложения $T = 2\pi$ , значит $l = \pi$ .

$a_0 = \frac{1}{l} \int_{-l}^{l} f(x) \, dx = 2$ (вычисления, конечно же, пропустим)

$a_n = \frac{1}{l} \int_{-l}^{l} f(x) \cos\left(\frac{\pi n}{l} x\right) \, dx = 0$

$b_n = \frac{1}{l} \int_{-l}^{l} f(x) \sin\left(\frac{\pi n}{l} x\right) \, dx = - \frac{2 \cdot (-1)^n}{n}$

Подставляем коэффициенты в формулу: $f(x) \sim \frac{a_0}{2} + \sum_{n=1}^{\infty} \left( a_n \cos\left(\frac{2\pi n}{T} x\right) + b_n \sin\left(\frac{2\pi n}{T} x\right) \right) = 1 - 2\sum_{n=1}^{\infty} \frac{(-1)^n \sin(nx)}{n} = S(x)$

Теперь к построению.

На центральном отрезке $(-\pi, \pi)$ ряд Фурье сходится к самой функции $f(x) = x + 1$ . Теперь немного порассуждаем о природе рассматриваемого тригонометрического разложения. В ряд Фурье входят только периодические функции (константа, синусы и косинусы), поэтому сумма ряда тоже представляет собой периодическую функцию.

Что это значит в нашем конкретном примере? А это обозначает то, что сумма ряда – непременно периодична и наш отрезок интервала обязан бесконечно повторяться слева и справа.

Построим частичную сумму ряда. $S(x) = 1 - 2\sum_{n=1}^{\infty} \frac{(-1)^n \sin(nx)}{n} = 1 - 2 \cdot (\frac{(-1)^1 \sin(x)}{1} + \frac{(-2)^2 \sin(x)}{2} + \frac{(-3)^3 \sin(x)}{3} + \frac{(-4)^4 \sin(x)}{4} + \ldots) = 1 - 2 \cdot (-\sin(x) + \frac{\sin(2x)}{2} - \frac{\sin(3x)}{3} + \frac{\sin(4x)}{4} - \ldots)$

Откуда получаем, что $S_2(x) = 1 + 2\sin(x) - \sin(2x)$

Особый интерес представляют точки разрыва 1-го рода. В таких точках ряд Фурье сходится к изолированным значениям, которые расположены ровнёхонько посередине «скачка» разрыва (красные точки на чертеже). Как узнать ординату этих точек? Сначала найдём ординату «верхнего этажа»: для этого вычислим значение функции в крайней правой точке центрального периода разложения: . Чтобы вычислить ординату «нижнего этажа» проще всего взять крайнее левое значение этого же периода: $f(\pi) = -\pi + 1$ . Ордината среднего значения – это среднее арифметическое суммы «верха и низа»: $y = \frac{f(\pi) + f(-\pi)}{2} = 1$ . Приятным является тот факт, что при построении чертежа вы сразу увидите, правильно или неправильно вычислена середина.

# Диапазон значений для графика частичной суммы
full_linspace = np.linspace(-3 * Pi_, 3 * Pi_, 400)

# Диапазоны значений (прописанные явно) для графика суммы ряда
x_linspaces = [np.linspace(-3 * Pi_, -Pi_, 400), # Убавляем период
               np.linspace(-Pi_, Pi_, 400),
               np.linspace(Pi_, 3 * Pi_, 400)] # Добавляем период

S_2 = 1 + 2 * np.sin(full_linspace) - np.sin(2 * full_linspace)

S = [x_linspaces[0] + 1 + 2 * Pi_, # Убавляем период
     x_linspaces[1] + 1,
     x_linspaces[2] + 1 - 2 * Pi_] # Добавляем период

plt.figure(figsize=(10, 6))
plt.plot(
  full_linspace,
  S_2,
  label=r'$S_2 = 1 + 2\sin(x) - \sin(2x)$',
  color='blue'
)

# Флаг для легенды
label_added = False

for i in range(3):
    plt.plot(
      x_linspaces[i],
      S[i],
      color='orange',
      label=(r'$f(x) = x + 1 (периодическая)$' if not label_added else "")
    )
    label_added = True

points_x = [np.pi, -np.pi, 3*np.pi, -3*np.pi] # Те самые точки разрыва первого родаs
points_y = [1, 1, 1, 1] # Те самые точки разрыва первого рода
plt.scatter(points_x, points_y, color='red', marker='o')

plt.title('Графики функций $S_2$ и $f(x)$')
plt.xlabel('$x$')
plt.ylabel('Значение функции')
plt.axhline(0, color='black', linewidth=0.5, ls='--')
plt.axvline(0, color='black', linewidth=0.5, ls='--')
plt.grid()
plt.legend()
plt.xlim(-10, 10)
plt.ylim(-2.5, 5)

plt.show()

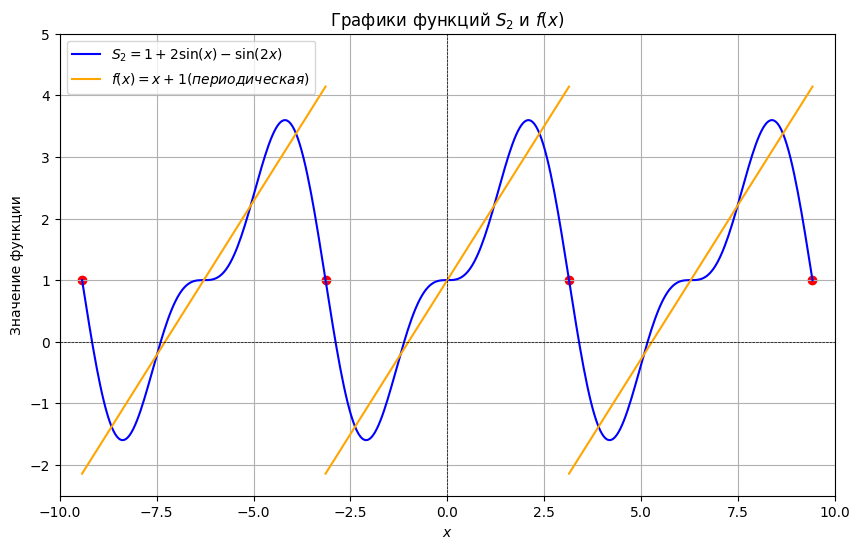
Важно понимать, что график сделан исключительно учебным и максимально упрощенным (легким для понимания, что же происходит в коде). На практике обычно достаточно изобразить три периода разложения, как это сделано на чертеже. В действительности же график уходит вдаль влево и вправо.

Задача 1 (1 балл)

А теперь найдите частичную сумму ряда $S_3(x)$ , $S_{10}(x)$ (очевидно, руками это не нужно делать) и постройте ее график. Какая из них лучше приближает $f(x)$ ? Для количественной оценки точности приближения вычислите среднюю абсолютную ошибку (MAE, Mean Absolute Error) для каждой частичной суммы:

MAE(f(x), S_{n}(x)) = \frac{1}{M}\sum_{i = 1}^{M}\left|f(x_i) - S_{n}(x_i)\right|

def MAE(S_n, f, n, linspace):
    return sum(abs(f(linspace) - S_n(n, linspace))) / len(linspace)

def fetch_S(n, x):
    return 1 - 2 * sum([(-1) ** i * np.sin(i * x) / i for i in range(1, n + 1)])

def plot_S(n):
    full_linspace = np.linspace(-3 * Pi_, 3 * Pi_, 400)

    x_linspaces = [np.linspace(-3 * Pi_, -Pi_, 400),
                  np.linspace(-Pi_, Pi_, 400),
                  np.linspace(Pi_, 3 * Pi_, 400)]

    S_n = fetch_S(n, full_linspace)

    S = [x_linspaces[0] + 1 + 2 * Pi_,
        x_linspaces[1] + 1,
        x_linspaces[2] + 1 - 2 * Pi_]

    plt.figure(figsize=(10, 6))
    plt.plot(
      full_linspace,
      S_n,
      label='$S_{' + str(n) + '}$',
      color='blue'
    )

    label_added = False
    for i in range(3):
        plt.plot(
          x_linspaces[i],
          S[i],
          color='orange',
          label=(r'$f(x) = x + 1 (периодическая)$' if not label_added else "")
        )
        label_added = True

    points_x = [np.pi, -np.pi, 3*np.pi, -3 * np.pi]
    points_y = [1, 1, 1, 1]
    plt.scatter(points_x, points_y, color='red', marker='o')

    plt.title('Графики функции $S_{' + str(n) + '}$ и $f(x)$')
    plt.xlabel('$x$')
    plt.ylabel('Значение функции')
    plt.axhline(0, color='black', linewidth=0.5, ls='--')
    plt.axvline(0, color='black', linewidth=0.5, ls='--')
    plt.grid()
    plt.legend()
    plt.xlim(-10, 10)
    plt.ylim(-2.5, 5)

    plt.show()

    # considering just one period because it is identical otherwise, and I don't have to deal with periodicity
    print(MAE(fetch_S, lambda x: x + 1, n, np.linspace(-Pi_, Pi_, 400)))

plot_S(3)
plot_S(20)

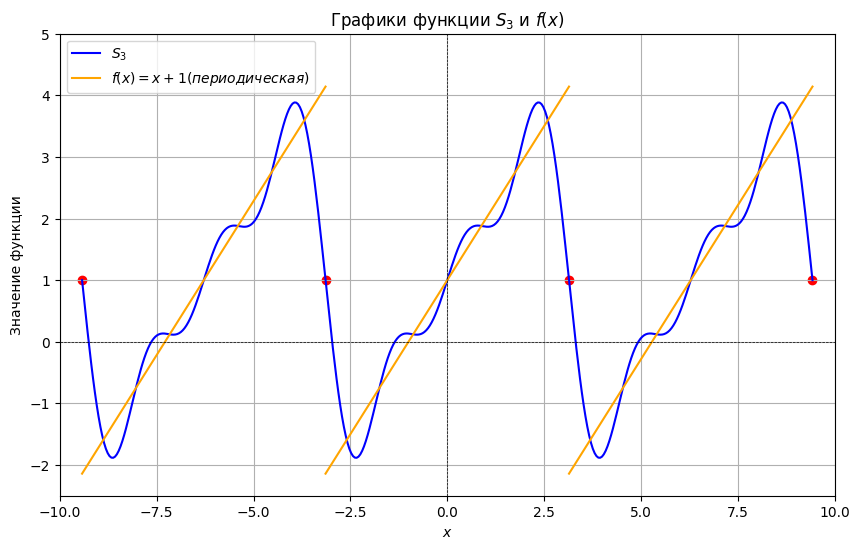
0.4648799866959148

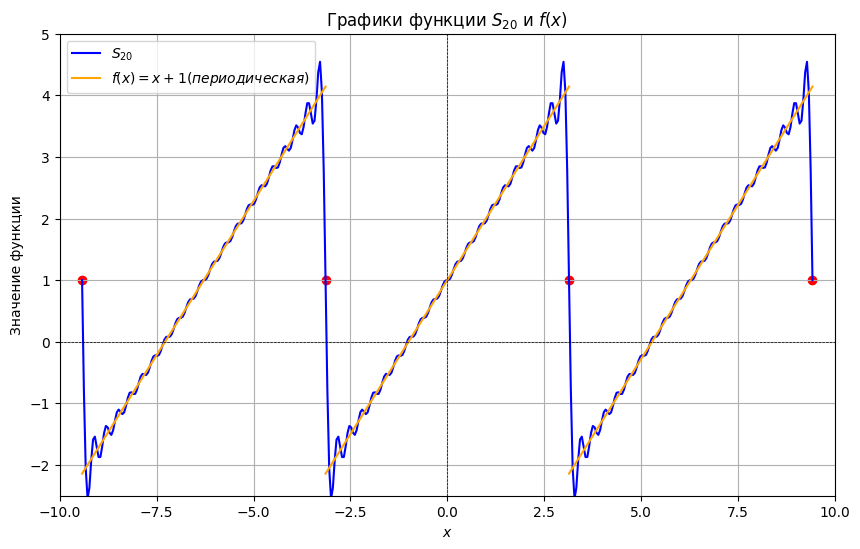
0.1209855223349181

MAE for $S_3$ is $\approx 1.465$ , whereas MAE for $S_{10}$ is $\approx 0.121$ . This implies that the second partial sum approximates function $f(x)$ considerably better, which can as well be observed in the graph.

Задача 2 (2 балла)

Реализуйте функции по поиску коэффициентов $a_{0}, a_{n}, b_{n}$

import scipy.integrate as spi

def get_a_0(T, f):
  l = T / 2
  result, _ = spi.quad(f, -l, l)
  return 1 / l * result

Протестируйте ваше решение, запустив ячейку кода ниже

def test_get_a_0():
  x = sp.symbols('x')
  def fu_1(x):
    return x + 1
  def fu_2(x):
    return sp.cos(x) + x**2 + x
  if (get_a_0(30, fu_2) - 150.086705 < 1e-6):
    print("TEST 1 GOOD")
  else:
    print("TEST 2 BAD")
  if (get_a_0(2*Pi_, fu_1) - 2.0 < 1e-6):
    print("TEST 1 GOOD")
  else:
    print("TEST 2 BAD")
test_get_a_0()

TEST 1 GOOD
TEST 1 GOOD

def get_a_n(T, f, n):
  l = T / 2
  result, _ = spi.quad(lambda x: f(x) * np.cos(np.pi * n / l * x), -l, l)
  return 1 / l * result

Протестируйте ваше решение, запустив ячейку кода ниже

def test_get_a_n():
  x = sp.symbols('x')
  def fu_1(x):
    return x + 1
  def fu_2(x):
    return sp.cos(x) + x**2 + x
  if (get_a_n(30, fu_2, 5) - (-2.75020582772811) < 1e-6):
    print("TEST 1 GOOD")
  else:
    print("TEST 1 BAD")
  if (get_a_n(2*Pi_, fu_1, 2) - (-7.06789929214115e-17) < 1e-6):
    print("TEST 2 GOOD")
  else:
    print("TEST 2 BAD")
test_get_a_n()

TEST 1 GOOD
TEST 2 GOOD

def get_b_n(T, f, n):
  l = T / 2
  result, _ = spi.quad(lambda x: f(x) * np.sin(np.pi * n / l * x), -l, l)
  return 1 / l * result

Протестируйте ваше решение, запустив ячейку кода ниже

def test_get_b_n():
  x = sp.symbols('x')
  def fu_1(x):
    return x + 1
  def fu_2(x):
    return sp.cos(x) + x**2 + x
  if (get_b_n(Pi_, fu_2, 5) - 0.2 < 1e-6):
    print("TEST 1 GOOD")
  else:
    print("TEST 1 BAD")
  if (get_b_n(2*Pi_, fu_1, 10) - (-0.2) < 1e-6):
    print("TEST 2 GOOD")
  else:
    print("TEST 2 BAD")
test_get_b_n()

TEST 1 GOOD
TEST 2 GOOD

Задача 3 (2 балла)

Разложите функцию $f(x)$ в ряд Фурье и постройте график частичной суммы ряда $S_3(x)$ .

f(x) = \begin{cases} -7, & \text{если } -2 < x \leq 0 \\ 6 - x, & \text{если } 0 < x \leq 2 \end{cases}

Решение оформите либо в текстовом виде в ячейке либо приложите фотографию с решением.

a_0 = \frac{1}{2} \int\limits_{-2}^{2} f(x)= -\frac{7}{2}x \Biggm|_{-2}^0 + \frac{1}{2}\left(6x - \frac{x^2}{2}\right)\Biggm|_{0}^2=(-14+10)/2 = -2

$$\begin{align*} a_n &= \frac{1}{2} \int\limits_{-2}^{2} f(x) \cos\left(\frac{\pi}{n} x\right) , dx =-\frac{7}{2} \int\limits_{-2}^{0} \cos\left(\frac{\pi}{n} x\right) , dx+\frac{1}{2}\int\limits_{0}^2(6-x)\cos\left(\frac{\pi}{n} x\right), dx\ &=-\frac{1}{2}\int\limits_{0}^2\cos\left(\frac{\pi}{n}x\right), dx+\frac{1}{2}\int\limits_0^2x\cos\left(\frac{\pi}{n}x\right), dx=-\frac{n}{2\pi}\left((x+1)\sin\left(\frac{\pi}{n}x\right)\Biggm|_0^2+\int\limits^2_0\sin\frac{\pi}{n}x, dx\right)\ &=-\frac{n}{2\pi}\left((x+1)\sin\left(\frac{\pi}{n}x\right)-\frac{n}{\pi}\cos\left(\frac{\pi}{n}x\right)\right)\Biggm|_0^2=-\frac{n}{2\pi}\left(\sin\frac{2\pi}{n}-\frac{n}{\pi}\cos\frac{2\pi}{n}+\frac{n}{\pi}\right)\ &=\frac{n^{2}}{2\pi^2}\left(1-\cos{\frac{2 \pi}{n}}\right)-\frac{3n}{2 \pi}\sin{\frac{2 \pi}{n}}\ a_1&=\frac{1^{2}}{2\pi^2}\left(1-\cos{\frac{2 \pi}{1}}\right)-\frac{3\cdot1 }{2 \pi}\sin{\frac{2 \pi}{1}}=0\ a_2&=\frac{2^{2}}{2\pi^2}\left(1-\cos{\frac{2 \pi}{2}}\right)-\frac{3\cdot 2}{2 \pi}\sin{\frac{2 \pi}{2}} = \frac{4}{\pi^{2}}\ a_3&=\frac{3^{2}}{2\pi^2}\left(1-\cos{\frac{2 \pi}{3}}\right)-\frac{3\cdot 3}{2 \pi}\sin{\frac{2 \pi}{3}} = - \frac{9 (\sqrt{3} \pi - 3)}{4 \pi^{2}}

\end{align*}$$

\begin{align*} b_n &= \frac{1}{2} \int\limits_{-2}^{2} f(x) \sin\left(\frac{\pi}{n} x\right) \, dx =-\frac{7}{2} \int\limits_{-2}^{0} \sin\left(\frac{\pi}{n} x\right)\, dx +\frac{1}{2}\int\limits_{0}^2(6-x)\sin\left(\frac{\pi}{n} x\right)\, dx\\ &= \frac{7n}{2\pi}\cos\left(\frac{\pi}{n} x\right)\Biggm|_{-2}^{0} + -\frac{3n}{\pi}\cos\left(\frac{\pi}{n} x\right)\Biggm|_{0}^{2} +\frac{nx}{2\pi}\cos\left(\frac{\pi}{n} x\right) - \frac{n^2}{2\pi^2}\sin\left(\frac{\pi}{n} x\right)\Biggm|_{0}^{2} \\ &= \frac{7n}{2\pi}\left(1-\cos\frac{2\pi}{n}\right) + \frac{3n}{\pi}\left(1-\cos\frac{2\pi}{n}\right) - \frac{1}{2}\left(\frac{n^2}{\pi^2}\sin\frac{2\pi}{n} - \frac{2n}{\pi}\cos\frac{2\pi}{n}\right)\\ &= \frac{7n}{2\pi} - \frac{7n}{2\pi}\cos\frac{2\pi}{n} + \frac{3n}{\pi} - \frac{3n}{\pi}\cos\frac{2\pi}{n} - \frac{n^2}{2\pi^2}\sin\frac{2\pi}{n} + \frac{n}{\pi}\cos\frac{2\pi}{n} \\ &= \frac{13n}{2\pi} - \frac{11n}{2\pi}\cos\frac{2\pi}{n} - \frac{n^2}{2\pi^2}\sin\frac{2\pi}{n}\\ b_1&=\frac{13\cdot 1}{2\pi} - \frac{11\cdot 1}{2\pi}\cos\frac{2\pi}{1} - \frac{1^2}{2\pi^2}\sin\frac{2\pi}{1} = \frac{1}{\pi}\\ b_2&=\frac{13\cdot 2}{2\pi} - \frac{11\cdot 2}{2\pi}\cos\frac{2\pi}{2} - \frac{2^2}{2\pi^2}\sin\frac{2\pi}{2}= \frac{24}{\pi}\\ b_3&=\frac{13\cdot 3}{2\pi} - \frac{11\cdot 3}{2\pi}\cos\frac{2\pi}{3} - \frac{3^2}{2\pi^2}\sin\frac{2\pi}{3}= \frac{3}{4\pi^2}\left(37\pi - 3\sqrt{3}\right)\end{align*}

\begin{align*} f(x) &\sim -1 + \frac{1}{\pi} \sin\left(\frac{\pi x}{2}\right) +\frac{4}{\pi^2} \cos\left(\pi x\right) +\frac{24}{pi}\sin\left(\pi x\right) - \frac{9 (\sqrt{3} \pi - 3)}{4 \pi^{2}}\cos\left(\frac{3\pi x}{2}\right) + \frac{3}{4\pi^2}\left(37\pi - 3\sqrt{3}\right) \sin\left(\frac{3\pi x }{2}\right) \end{align*}

Задача 4 (2 балла)

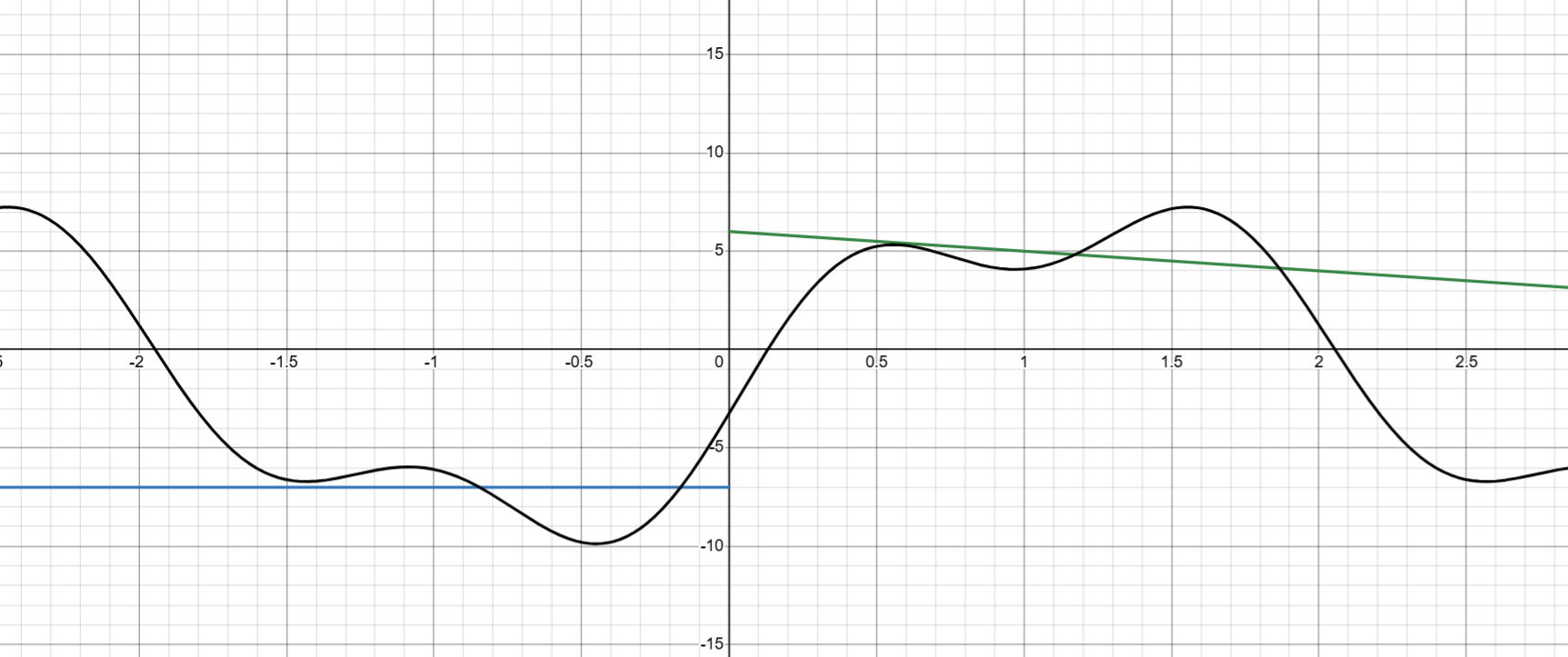
Выполните Задание 3, но уже в коде, пользуясь исключительно Python

def get_S_n(T, f, n, x):
    return get_a_0(T, f) / 2 + sum(get_a_n(T, f, i) * np.cos(2 * np.pi * i / T * x) + get_b_n(T, f, i) * np.sin(2 * np.pi * i / T * x) for i in range(1, n+1))

def get_a_0(T, f):
    l = T / 2
    result, _ = spi.quad(f, -l, l)
    return result / l

def get_a_n(T, f, n):
    l = T / 2
    k = np.pi * n / l
    result, _ = spi.quad(lambda x: f(x) * np.cos(k * x), -l, l)
    return result / l

def get_b_n(T, f, n):
    l = T / 2
    k = np.pi * n / l
    result, _ = spi.quad(lambda x: f(x) * np.sin(k * x), -l, l)
    return result / l

def get_S_n(T, f, n, x):
    x = np.array(x)
    S = get_a_0(T, f) / 2
    for i in range(1, n+1):
        S += (
            get_a_n(T, f, i) * np.cos(2 * np.pi * i / T * x)
            + get_b_n(T, f, i) * np.sin(2 * np.pi * i / T * x)
        )
    return S

def plot_S(T, f, n):
    l = T / 2
    full_linspace = np.linspace(-l, l, 400)

    S_n = get_S_n(T, f, n, full_linspace)

    S = f(full_linspace)

    plt.figure(figsize=(10, 6))
    plt.plot(
      full_linspace,
      S_n,
      label='$S_{' + str(n) + '}$',
      color='blue'
    )

    plt.plot(
      full_linspace,
      S,
      color='orange',
      label=(r'$f(x)$')
    )

    plt.title('Графики функции $S_{' + str(n) + '}$ и $f(x)$')
    plt.xlabel('$x$')
    plt.ylabel('Значение функции')
    plt.axhline(0, color='black', linewidth=0.5, ls='--')
    plt.axvline(0, color='black', linewidth=0.5, ls='--')
    plt.grid()
    plt.legend()

    plt.show()

def func(x):
    x = np.array(x)
    y = np.zeros_like(x)

    y[(x >= -2) & (x <= 0)] = -7
    y[(x > 0) & (x <= 2)] = 6 - x[(x > 0) & (x <= 2)]

    return y

plot_S(4, func, 3)

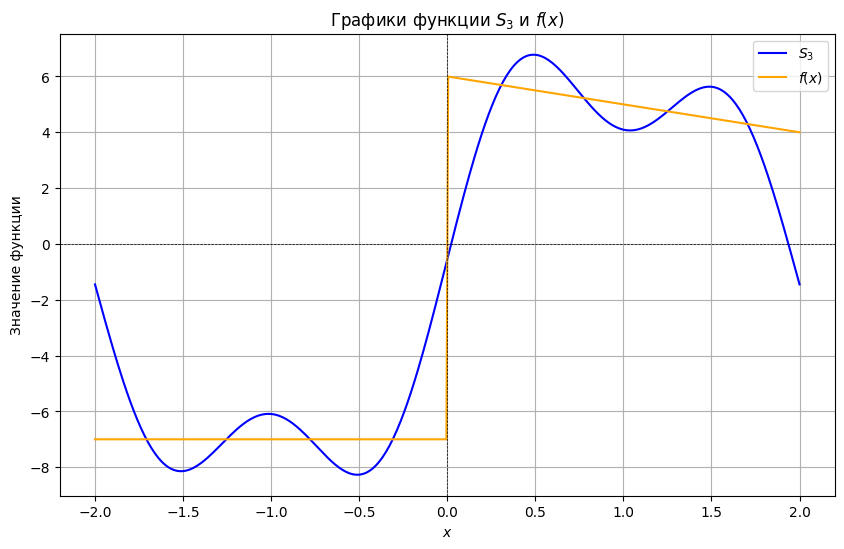
# also added this for visualization
plot_S(4, func, 100)

C:\Users\artemis\AppData\Local\Temp\ipykernel_18096\2693629959.py:18: IntegrationWarning: The maximum number of subdivisions (50) has been achieved.
  If increasing the limit yields no improvement it is advised to analyze 
  the integrand in order to determine the difficulties.  If the position of a 
  local difficulty can be determined (singularity, discontinuity) one will 
  probably gain from splitting up the interval and calling the integrator 
  on the subranges.  Perhaps a special-purpose integrator should be used.
  result, _ = spi.quad(lambda x: f(x) * np.sin(k * x), -l, l)
C:\Users\artemis\AppData\Local\Temp\ipykernel_18096\2693629959.py:12: IntegrationWarning: The maximum number of subdivisions (50) has been achieved.
  If increasing the limit yields no improvement it is advised to analyze 
  the integrand in order to determine the difficulties.  If the position of a 
  local difficulty can be determined (singularity, discontinuity) one will 
  probably gain from splitting up the interval and calling the integrator 
  on the subranges.  Perhaps a special-purpose integrator should be used.
  result, _ = spi.quad(lambda x: f(x) * np.cos(k * x), -l, l)

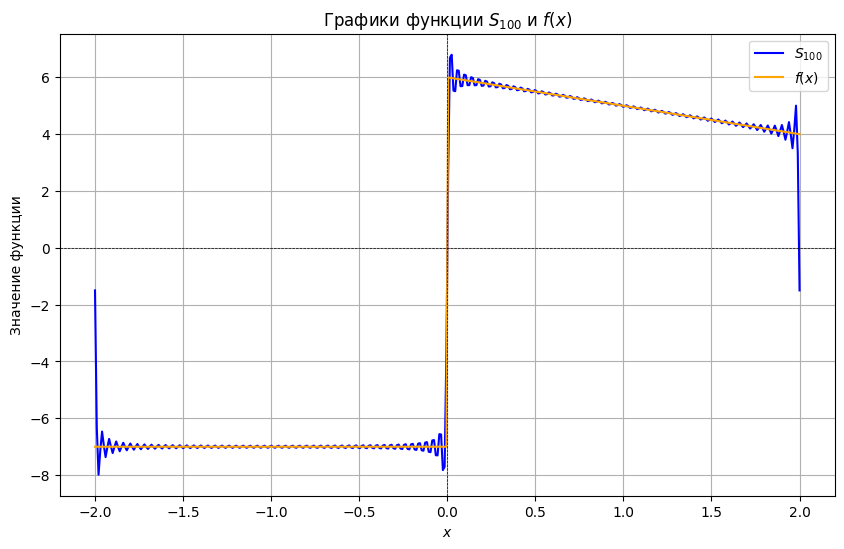
Часть 2. Фильтрация шума с помощью дискретного преобразования Фурье¶

Пользоваться библиотечными функциями fft и ifft запрещено.

В этом разделе мы рассмотрим применение дискретного преобразования Фурье (DFT) для фильтрации шума из аудиосигнала. Мы сгенерируем чистый сигнал, добавим к нему шум, а затем с помощью DFT удалим шумовые компоненты и восстановим исходный сигнал.

Цели работы:

Рассмотреть принцип действия дискретного преобразования Фурье.
Научиться применять DFT для анализа и фильтрации сигналов.
Получить практический опыт в обработке аудиосигналов с помощью Python и библиотек NumPy и SciPy.

Мы будем работать с библиотеками scipy и soundfile

Генерация чистого сигнала¶

Теперь давайте сгенерируем чистый синусоидальный сигнал с заданными параметрами частоты, длительности и частоты дискретизации. Это позволит нам иметь базовый сигнал для дальнейшего анализа и добавления шума.

Сгенерируем чистый синусоидальный сигнал с частотой 400 Гц и длительностью 5 секунд:

def generate_sine_wave(freq, sample_rate, duration):
    x = np.linspace(0, duration, int(sample_rate*duration), endpoint=False)
    y = np.sin(2 * np.pi * freq * x)
    return x, y

sample_rate = 44100
duration = 5
frequency = 400

time, clean_signal = generate_sine_wave(frequency, sample_rate, duration)

Визуализируем сигнал:

plt.figure(figsize=(10, 4))
plt.plot(time[:1000], clean_signal[:1000])
plt.title("Чистый синусоидальный сигнал (400 Гц)")
plt.xlabel("Время [с]")
plt.ylabel("Амплитуда")
plt.grid(True)
plt.show()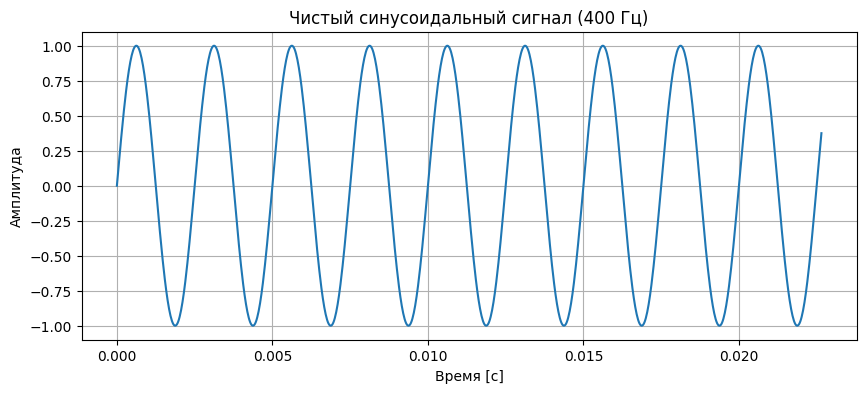

Воспользуемся возможностями Jupyter Notebook для прослушивания сигнала:

Audio(clean_signal, rate=sample_rate)

Добавление шума к сигналу¶

На этом этапе мы должны сгенерировать синусоидальный шум определенной частоты и добавить его к чистому сигналу, чтобы смоделировать зашумленный сигнал, с которым часто приходится работать в реальных условиях.

Сгенерируем шумовой сигнал с частотой 1500 Гц и добавим его к нашему чистому сигналу:

noise_frequency = 1500
noise_amplitude = 0.5

_, noise_signal = generate_sine_wave(noise_frequency, sample_rate, duration)
noise_signal *= noise_amplitude

noisy_signal = clean_signal + noise_signal

Визуализируем шум:

plt.figure(figsize=(10, 4))
plt.plot(time[:1000], noisy_signal[:1000])
plt.title("Зашумленный сигнал")
plt.xlabel("Время [с]")
plt.ylabel("Амплитуда")
plt.grid(True)
plt.show()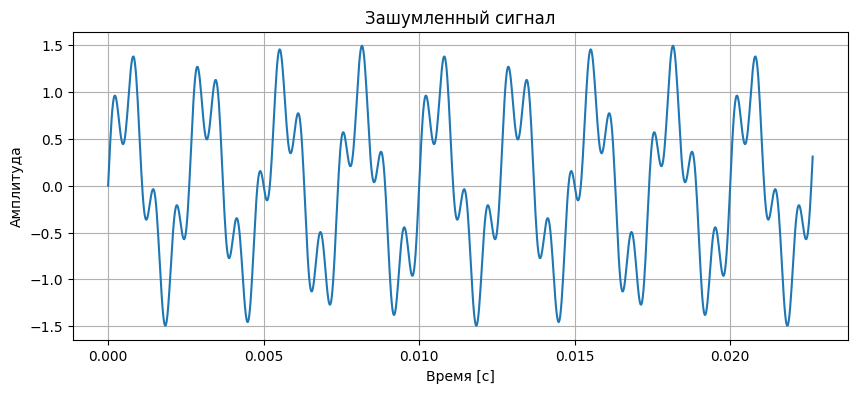

Прослушаем получившийся зашумленный сигнал:

Audio(noisy_signal, rate=sample_rate)

Применение дискретного преобразования Фурье для определения спектра звуковых сигналов¶

Наконец перейдем к части где мы и будем использовать наши знания о дискретном преобразовании Фурье на практике.

Теория:¶

Дискретное Преобразование Фурье (DFT) позволяет разложить сигнал, представленный в виде временной последовательности, на составляющие частоты. Процесс преобразования временной последовательности в частотную описывается формулой:

X_k = \sum_{n=0}^{N-1} x_n \cdot e^{-i 2\pi kn/N}

где:

$X_k$ — комплексное значение, соответствующее амплитуде и фазе частоты $k$ ,
$x_n$ — значение сигнала во временной точке $n$ ,
$N$ — общее количество точек сигнала (длина массива),
$k$ — номер частоты, которую мы хотим вычислить.

Формула предполагает, что сигнал рассматривается как сумма синусоидальных волн с разными частотами и амплитудами. Каждая частотная компонента может быть извлечена, умножая исходный сигнал на соответствующую экспоненту.

Понятно, что в таком виде DFT будет работать за $O(N^2)$ , потому что нам для каждой частоты $k$ надо сделать проход по $n$ . Очевидно, что такая асимптотика нам не подходит и мы попытаемся понять и реализовать быстрое преобразование Фурье.

Для начала покажем, что у DFT выполняется периодичность:¶

X_{N+k} = X_k \quad \text{для всех целых } k

Начнём с определения:

X_{N+k} = \sum_{n=0}^{N-1} x_n \cdot e^{-i 2\pi (N+k)n/N}

Разложим экспоненту, используя свойства степеней:

X_{N+k} = \sum_{n=0}^{N-1} x_n \cdot e^{-i 2\pi Nn/N} \cdot e^{-i 2\pi kn/N}

= \sum_{n=0}^{N-1} x_n \cdot e^{-i 2\pi n} \cdot e^{-i 2\pi kn/N}

Применим тождество Эйлера для полного оборота на комплексной плоскости:

e^{-i 2\pi n} = \cos(2\pi n) - i \sin(2\pi n) = 1

это верно для любого целого числа $n$ , так как полный оборот вокруг единичного круга равен единице.

Подставим этот факт в соотношение:

X_{N+k} = \sum_{n=0}^{N-1} x_n \cdot 1 \cdot e^{-i 2\pi kn/N} = \sum_{n=0}^{N-1} x_n \cdot e^{-i 2\pi kn/N} = X_k

Таким образом, спектр повторяется с периодом $N$ . Это означает, что нам нужно вычислить только первые $N$ значений.

От DFT к FFT: Алгоритм Кули-Тьюки¶

Оригинальную статью можете прочитать здесь, но я перескажу нужное ниже.

Основная идея этого алгоритма - это разделить исходную сумму на две меньшие суммы, каждая из которых снова похожа на DFT. Одна сумма будет четной $n = 2m$ , другая нечетной $n = 2m + 1$ , где $m = 0, 1, \ldots, N/2-1$ .

X_k = \sum_{n=0}^{N-1} x_n \cdot e^{-i 2\pi kn/N}

Разделение на четные и нечетные индексы
$X_k = \sum_{m=0}^{N/2-1} x_{2m} \cdot e^{-i 2\pi k(2m)/N} + \sum_{m=0}^{N/2-1} x_{2m+1} \cdot e^{-i 2\pi k(2m+1)/N}$
Преобразование экспонент
Для первого слагаемого:
$e^{-i 2\pi k(2m)/N} = e^{-i 2\pi km/(N/2)}$
Для второго слагаемого:
$e^{-i 2\pi k(2m+1)/N} = e^{-i 2\pi k(2m)/N} \cdot e^{-i 2\pi k/N} = e^{-i 2\pi km/(N/2)} \cdot e^{-i 2\pi k/N}$
Теперь введём удобное обозначение - поворотный множитель:
$W_N^k = e^{-i 2\pi k/N}$

Подставим преобразованные экспоненты:
$X_k = \sum_{m=0}^{N/2-1} x_{2m} \cdot e^{-i 2\pi km/(N/2)} + W_N^k \sum_{m=0}^{N/2-1} x_{2m+1} \cdot e^{-i 2\pi km/(N/2)}$
Что получили?
Обратим внимание, что каждая сумма — это DFT размера $N/2$ :
$E_k = \sum_{m=0}^{N/2-1} x_{2m} \cdot e^{-i 2\pi km/(N/2)} \quad \text{(DFT четных элементов)}$
$O_k = \sum_{m=0}^{N/2-1} x_{2m+1} \cdot e^{-i 2\pi km/(N/2)} \quad \text{(DFT нечетных элементов)}$
где индекс $k$ берется в диапазоне $0 \leq k < N/2$ .
То есть для первой половины спектра $X_k$ вычисляется как:
$X_k = E_k + W_N^k \cdot O_k$
А что происходит со второй половиной?
Ведь мы асимптотически пока еще никак не улучшили наш алгоритм. Мы по прежнему имеем $O(N^2)$ . Дело в том, что мы доказали периодичность DFT, но ни разу не применяли ее.
Но ведь для ДПФ размера $N/2$ также имеет место периодичность:
$E_{k + N/2} = E_k, \quad O_{k + N/2} = O_k$
это следует из того же доказательства, что и раньше.
Для поворотного множителя при сдвиге на $N/2$ :
$W_N^{k+N/2} = e^{-i 2\pi (k+N/2)/N} = e^{-i 2\pi k/N} \cdot e^{-i 2\pi (N/2)/N}$
$= e^{-i 2\pi k/N} \cdot e^{-i \pi} = e^{-i 2\pi k/N} \cdot (-1)$
$= -W_N^k$
Применим эти свойства:
$X_{k+N/2} = E_{k+N/2} + W_N^{k+N/2} \cdot O_{k+N/2}$
$= E_k + (-W_N^k) \cdot O_k$
$= E_k - W_N^k \cdot O_k \quad \text{для } k = 0, 1, \ldots, N/2-1$
Итог, для $k = 0, 1, \ldots, N/2-1$
$\begin{cases} X_k = E_k + W_N^k \cdot O_k \\ X_{k+N/2} = E_k - W_N^k \cdot O_k \end{cases}$

Задача 5 (1 балла)

Ваша задача описать, почему мы все таки улучшили асимптотику, то есть почему мы получили $O(n \cdot \log_2 N)$ .

Conclusion:

Ordinarily, binary $\log$ appears whenever on each iteration we reduce the number of steps to take by a factor of 2. In this approach, we compute halves of a DFT recursively to get a DFT of length $N$ . Since we can apply this indefinitely (within limits, ofc), we could reduce computational time of a DFT of length $N$ from $O(n)$ to $O(\log_2 N)$ , which is exactly what happens with the asymptotics, with one $N$ being replaced with $\log_2 N$ .

Условия применимости нашего алгоритма¶

Классический алгоритм Кули-Тьюки эффективен когда $N = 2^m$ для целого $m$ . Это потому, что:

На каждом шаге мы точно делим пополам
Получаем $\log_2 N$ уровней рекурсии
Нет остатков при делении

Поэтому для простоты мы будем дополнять входные данные нулями до ближайшей степени двойки (zero-padding). Легче всего использовать np.pad.

Задача 6 (3 балла)

Реализуйте цикл для вычисления каждого значения $X_k$ на основе временного сигнала $X_n$ .

def pad(signal):
    N = len(np.array(signal))
    M = 2 ** int(np.ceil(np.log2(N)))
    return np.pad(signal, (0, M - N), mode='constant')

def FFT(signal):
    return _FFT(pad(signal))

def _FFT(signal):
    signal = np.asarray(signal, dtype=complex)
    N = signal.shape[0]
    
    if N <= 1:
        return signal
    
    X_even = _FFT(signal[::2])
    X_odd  = _FFT(signal[1::2])

    k = np.arange(N//2)
    W_N_k = np.exp(-2j * np.pi * k / N)

    X = np.zeros(N, dtype=complex)
    X[:N//2] = X_even + W_N_k * X_odd
    X[N//2:] = X_even - W_N_k * X_odd

    return X

Постройте спектр амплитуд:

S = FFT(noisy_signal)
print(S)

[-0.     +0.j      9.1044-16.7024j 28.0755-18.1009j ... 39.5307 +2.9141j
 28.0755+18.1009j  9.1044+16.7024j]

Визуализация спектра:

N = len(S)

def fft_frequencies(N, d):
    k = np.arange(N)
    return np.where(k <= N // 2, k, k - N) / (N * d)

freqs = fft_frequencies(N, 1 / sample_rate)

plt.figure(figsize=(8,4))
plt.plot(freqs, S)

plt.xlabel("Frequency (Hz)")
plt.ylabel("Amplitude")
plt.xlim(0, noise_frequency + 100)
plt.title("Amplitude Spectrum")
plt.grid(True)
plt.show()

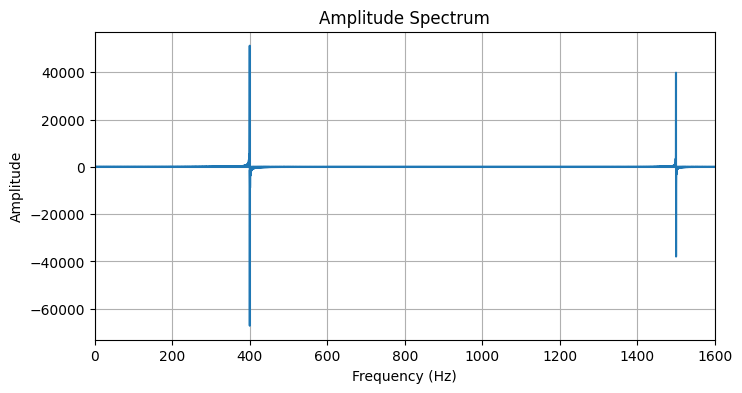
Если вы все сделали правильно то на графике вы заметите следующее:

Основной сигнал: Пик на частоте около 400 Гц - это чистая синусоида, которая была сгенерирована в начале.

Шум: Пик на частоте около 1500 Гц - это добавленный шум.

Симметричные пики справа: Вы также заметите, что на правой части графика (на частотах 40000+) появляются такие же пики - это не ошибка. Это отрицательные частоты, которые появляются в спектре DFT вещественного сигнала из-за периодичности и симметрии преобразования. Для вещественных сигналов вторая половина спектра является зеркальным отражением первой половины и не содержит новой информации.

Фильтрация шума в частотной области¶

На этом этапе мы должны удалить шумовую компоненту из сигнала, обнулив соответствующие частотные компоненты в спектре.

Задача 7 (3 балла)

Выведите индексы частоты шума и удалите шум из нашего сигнала:

window = 500
S[np.abs(freqs - noise_frequency) < window] = 0
S[np.abs(freqs + noise_frequency) < window] = 0

Сделайте визуализацию отфильтрованного спектра:

plt.figure(figsize=(8,4))
plt.plot(freqs, S)
plt.xlabel("Frequency (Hz)")
plt.ylabel("Amplitude")
plt.xlim(0, noise_frequency + 100)
plt.title("Amplitude Spectrum")
plt.grid(True)
plt.show()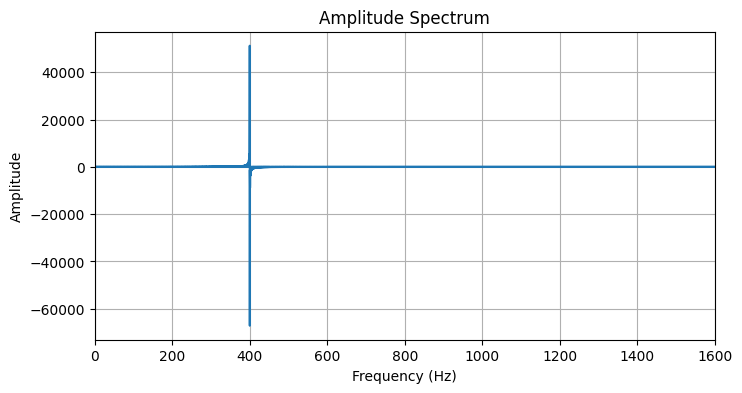

Если вы все сделали правильно то пик на частоте шума и его зеркальное отражение должны исчезнуть из спектра.

Обратное преобразование Фурье и восстановление сигнала¶

Теория:¶

В предыдущем разделе мы разложили сигнал из временной области в частотную область, используя формулу ДПФ:

X_k = \sum_{n=0}^{N-1} x_n \cdot e^{-i 2\pi kn/N}

Теперь нам нужно выполнить обратное преобразование — восстановить сигнал из его частотных компонент. Это описывается формулой Обратного Дискретного Преобразования Фурье (IDFT):

x_n = \frac{1}{N} \sum_{k=0}^{N-1} X_k \cdot e^{i 2\pi kn/N}

где:

$x_n$ — значение сигнала во временной точке $n$ после обратного преобразования,
$X_k$ — комплексное значение спектра на частоте $k$ ,
$N$ — общее количество точек сигнала (длина массива),
$k$ — номер частотного компонента.

Задача 8 (4 балла)

Преобразуйте отфильтрованный спектр обратно во временную область, получив очищенный от шума сигнал. При реализации функции IFFT ожидается, что вы будете следовать тому же принципу разделения пополам (алгоритм Кули-Тьюки), что и в обычном FFT.

Если вы решите использовать альтернативный подход через комплексное сопряжение, то обязательно приложите математическое доказательство его корректности, потому что без объяснения такой подход не будет засчитан.

def IFFT(signal):
    return _IFFT(signal) / signal.shape[0]

def _IFFT(signal_dft):
    signal_dft = np.asarray(signal_dft, dtype=complex)
    N = signal_dft.shape[0]

    if N <= 1:
        return signal_dft
    
    X_even = _IFFT(signal_dft[::2])
    X_odd  = _IFFT(signal_dft[1::2])
    
    k = np.arange(N//2)
    W_N_k = np.exp(2j * np.pi * k / N)
    
    X = np.zeros(N, dtype=complex)
    X[:N//2] = X_even + W_N_k * X_odd
    X[N//2:] = X_even - W_N_k * X_odd

    return X

Отфильтруйте сигнал:

restored_signal = IFFT(S)

Сделайте визуализацию отфильтрованного сигнала:

plt.figure(figsize=(10,4))
plt.plot(time[:1000], restored_signal[:1000])
plt.xlabel("Time")
plt.ylabel("Amplitude")
plt.title("Restored signal")
plt.grid(True)
plt.show()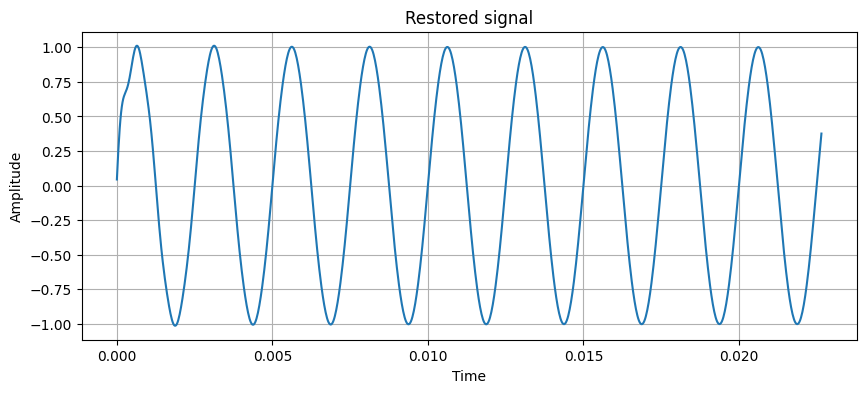

Как вы вероятно заметили спустя несколько попыток, очень сложно добиться полного удаления шума за счет собственного алгоритма, это и не требуется, важно чтобы ваш фильтр давал максимальное приближение к тому результату которого мы добиваемся, чтобы на практике мы не ощущали присутствия шума в звуковой дорожке.

Чтобы это проверить давайте выведем и прослушаем отфильтрованное аудио. Качество фильтрации шума оцените самостоятельно.

Прослушивание отфильтрованного сигнала

Audio(restored_signal, rate=sample_rate)

Конечно сложно в полной мере оценить насколько хорошо мы избавились от шума когда речь о синусоидных сигналах, поэтому в дальнейших задачах мы повторим наши действия уже на реальном аудио которое будет удобнее оценить на слух.

Сравнение сигналов¶

Задача 9 (1 балла)

Выведите графики исходного сигнала, зашумленного сигнала и отфильтрованного сигнала. Что вы видите? Сделайте вывод о проделанной работе.

plt.figure(figsize=(10,4))
plt.plot(time[:1000], clean_signal[:1000], label="clean signal")
plt.plot(time[:1000], restored_signal[:1000], label="restored signal")
plt.plot(time[:1000], noisy_signal[:1000], label="noisy signal")
plt.xlabel("Time")
plt.ylabel("Amplitude")
plt.title("Restored signal")
plt.grid(True)
plt.legend()
plt.show()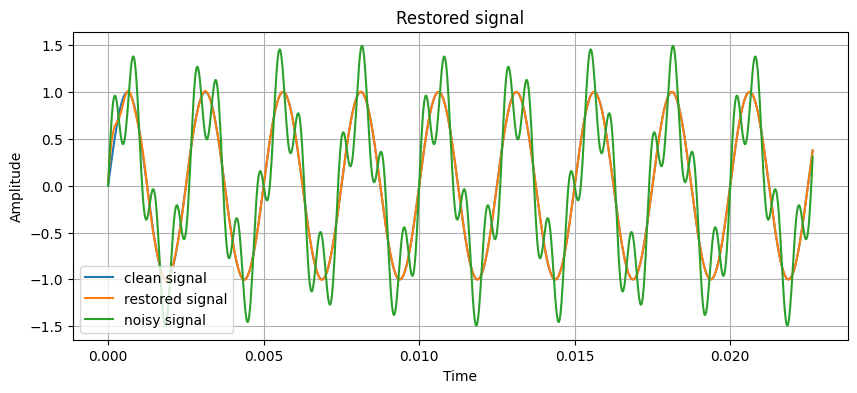

As it could be observed from the graph and the restored signal audio, we have cleaned the noisy signal quite well. The restored signal, of course, lies somewhere in-between the original signal and the noisy one, but it’s very similar to the clean signal than the latter. It might be possible to achieve a better result, but that’s not really the point here.

Overall, this part was really fun and engaging, and it’s really nice to see that everything actually works.

Спектрограммы¶

Для более удобного анализа сигнала во временно-частотной области постройте спектрограммы с использованием STFT (коротковременное преобразование Фурье)

Теория:¶

STFT решает проблему обычного FFT - он показывает не только какие частоты присутствуют в сигнале, но и когда они присутствуют. Идея проста: разбить длинный сигнал на короткие перекрывающиеся окна, применить к каждому окну оконную функцию (в нашем случае hann) для уменьшения артефактов на краях, а затем вычислить FFT для каждого окна отдельно. Результатом является матрица, где строки - это частоты, столбцы - это временные кадры, а значения показывают амплитуду спектра в каждый момент времени.

На визуализации это выглядит как тепловая карта, где яркие цвета указывают на сильные компоненты сигнала, а темные цвета - на слабые. Горизонтальные яркие линии на спектрограмме соответствуют стационарным компонентам (синусоидам, которые присутствуют на протяжении всего сигнала), поэтому вы ясно увидите горизонтальную линию на 400 Гц (основной сигнал) и еще одну горизонтальную линию на зашумленной спектрограмме. После применения фильтрации линия шума должна значительно ослабнуть или исчезнуть., оставив только основной сигнал.

Без нормальной оконной функции на краях каждого окна возникают разрывы, создающие артефакты в спектре. Оконная функция Hann плавно обнуляет сигнал на краях, избегая этих разрывов:

w(n) = 0.5 \left(1 - \cos\left(\frac{2\pi n}{N-1}\right)\right) \quad \text{для } n = 0, 1, \ldots, N-1

Это просто преобразованный косинус! График выглядит как колокол - максимум в центре (равен 1), нули на краях.

Для вычисления STFT используйте следующие параметры: nfft=1024 (размер FFT), winSize=1024 (размер оконной функции), hopSize=512 (размер шага сдвига, что соответствует 50% перекрытию окон), windowType="hann". Эти параметры обеспечивают хороший баланс между разрешением по времени и по частоте для анализа звуковых сигналов.

Задача 10 (4 балла)

Реализуйте класс спектрограммы. Пользоваться встроенной функцией stft запрещено.

class STFTTransformer:
    def __init__(self, nfft, winSize, hopSize, sampleRate, windowType="hann"):
        self.nfft = nfft
        self.winSize = winSize
        self.hopSize = hopSize
        self.windowType = windowType
        self.sampleRate = sampleRate

    def get_window(self):
        if self.windowType == "hann":
            n = np.arange(self.winSize)
            window = 0.5 * (1 - np.cos(2 * np.pi * n / (self.winSize - 1)))
        else:
            raise NotImplementedError("this window type isn't implemented oh nooo!!")
          
        return np.array(window)

    def __call__(self, wav):
        window = self.get_window()

        framecount = 1 + (len(wav) - self.winSize) // self.hopSize
        spectrogram = np.zeros((framecount, self.nfft), dtype=complex)

        for i in range(framecount):
            j = i * self.hopSize
            segment = wav[j:j + self.winSize]

            if len(segment) < self.winSize:
                segment = np.pad(segment, (0, self.winSize - len(segment)))

            segment = segment * window

            if self.winSize < self.nfft:
                segment = np.pad(segment, (0, self.nfft - self.winSize))

            spectrogram[i, :] = FFT(segment)

        return spectrogram

Реализуйте функцию для визуализации спектрограммы. Настоятельно рекомендуем использовать логарифмическую шкалу.

import numpy as np
import matplotlib.pyplot as plt

def plotSpectrogram(wav, stftTransformer, useMelScale=False):
    spectogram = stftTransformer(wav)

    framecount = spectogram.shape[0]
    nfft = spectogram.shape[1]
    time = np.arange(framecount) * stftTransformer.hopSize / stftTransformer.sampleRate
    freq = np.arange(nfft) * stftTransformer.sampleRate / nfft

    smol_value = 1e-12
    log_spec = 20 * np.log10(np.maximum(np.abs(spectogram).T, smol_value))

    plt.figure(figsize=(10, 4))
    plt.imshow(log_spec, origin='lower', aspect='auto', 
               extent=[time[0], time[-1], freq[0], freq[-1]])
    plt.xlabel("Time (s)")
    plt.ylabel("Frequency (Hz)")
    plt.title("Spectrogram")
    plt.tight_layout()
    plt.show()

Постройте спектрограммы для зашумленного и отфильтрованного сигнала:

nfft = 1024
winSize = 1024
hopSize = 512

trans = STFTTransformer(nfft, winSize, hopSize, sample_rate, windowType="hann")

plotSpectrogram(clean_signal, trans)
plotSpectrogram(noisy_signal, trans)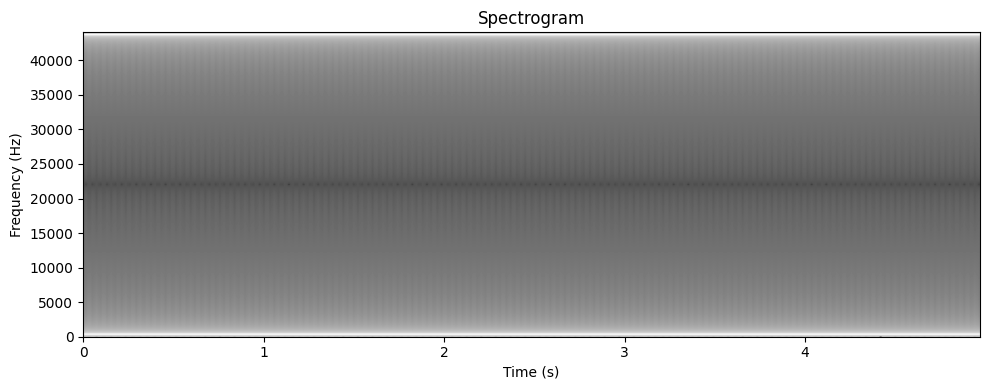

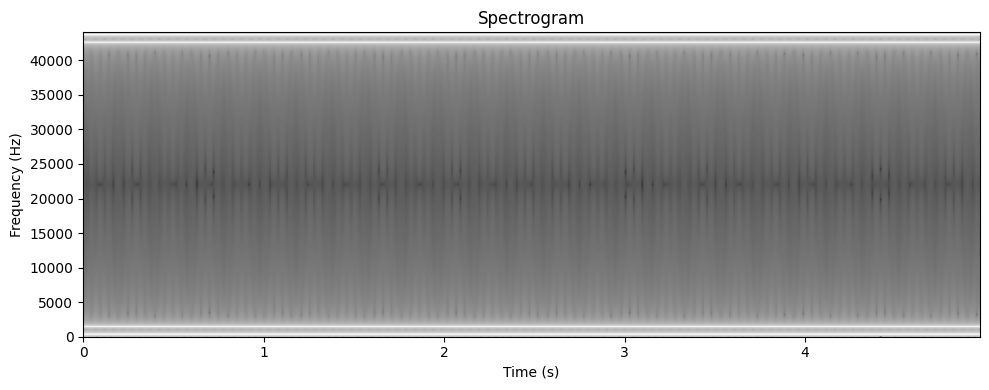
Какой вывод вы можете сделать?

Spectrograms are an excellent way to look at signals at once. Smoother signals yield smoother, less chaotic spectrograms, whereas high-frequency noise shows up as obvious interference which makes the spectrogram quite messy.

It is possible to figure out the noisiness of a signal by its spectrogram, as well as visualize it differently, fit more information in a comprehensive, compact way on the screen — effectively, it packs the sin wave in a smaller space by cleverly utilizing colors, which I would say is the main thing here, to create a more humanly-digestible visualization.

Применение фильтрации шума на примере реального голосового демо¶

В этом задании мы применим уже ранее разработанный алгоритм фильтрации шума к реальной голосовой записи, добавим синтетический шум на частоте 1100 Гц и отфильтруем его. Анализ мы выполним с помощью спектрограмм как в прошлом задании.

Для начала загрузим голосовую запись, которую можно скачать по ссылке

wav, sr = sf.read("./realVoiceMessage.wav")
wav = wav.mean(axis=-1)

print(f"Частота дискретизации: {sr}, Длительность: {wav.shape[-1] / sr} сек")

Частота дискретизации: 22050, Длительность: 19.470113378684808 сек

Задача 11 (5 баллов)

Постройте спектрограмму для оригинального голосового сигнала:

trans = STFTTransformer(nfft, winSize, hopSize, sr, windowType="hann")

plotSpectrogram(wav, trans)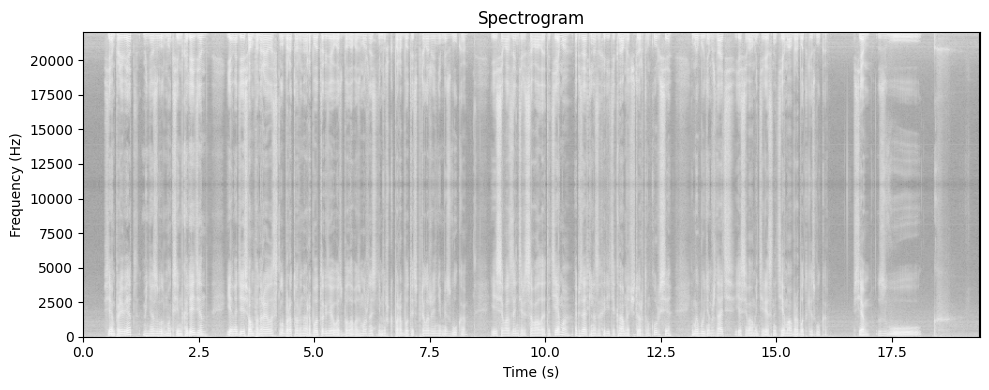

Прослушивание оригинального голосового сигнала. ОСТОРОЖНО, МОЖЕТ БЫТЬ ГРОМКО!

display(Audio(wav, rate=sr))

# it is RIDICULOUS how clearly the ЗВУУУУУУУУК 
# can be seen at the end of the spectrogram

Добавим синусоидальный шум на частоте 900 Гц к голосовому сигналу:

noise_frequency = 900
noise_amplitude = 0.5
_, noise_signal = generate_sine_wave(noise_frequency, sr, len(wav) / sr)
noise_signal *= noise_amplitude
noisy_wav = wav + noise_signal

Прослушивание смешанного с шумом голосового сигнала:

display(Audio(noisy_wav, rate=sr))

Постройте спектрограмму для зашумленного голосового сигнала:

plotSpectrogram(noisy_wav, trans)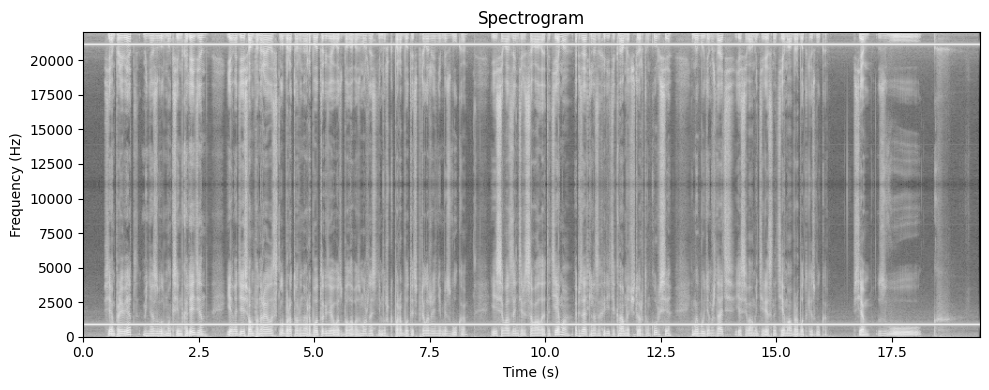

Теперь отфильтруйте шум из нашего голосового сигнала:

filtered_wav = FFT(noisy_wav)
window = 600
freqs = fft_frequencies(len(filtered_wav), 1 / sr)
filtered_wav[np.abs(freqs - noise_frequency) < window] = 0
filtered_wav[np.abs(freqs + noise_frequency) < window] = 0

Воспроизведите отфильтрованный голосовой сигнал:

restored_wav = IFFT(filtered_wav)[:wav.shape[0]]
display(Audio(restored_wav, rate=sr))

Выведите все 3 спекрограммы (начальная, с шумом и отфильтрованная) и проанализируйте их, сделав выводы о работе реализованного алгоритма с реальными голосовыми демо.

plotSpectrogram(wav, trans)
plotSpectrogram(noisy_wav, trans)
plotSpectrogram(restored_wav, trans)

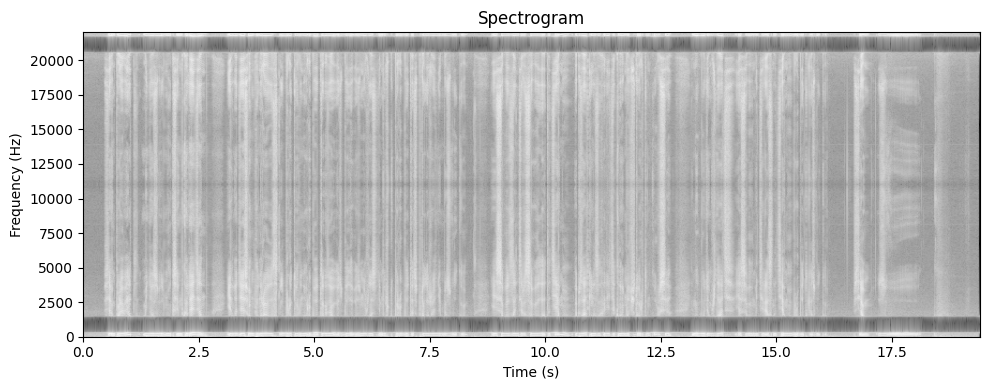
Clearly, adding the frequency of a stable sine wave to the main voice message has affected the spectogram by darkening in, since now there are extra fluctuations that have to pass through other signals while it resonates. Adding noise has also created a peak at a certain frequency, data around which we have deleted, thus reverting the voice message to a state where it doesn’t have as much noise anymore (notice how the spectrogram has lightened, too).

Spectral Subtraction - практическое удаление фонового шума¶

До этого мы удаляли лишь одну синусоиду. Но в реальности шум присутствует на всех частотах одновременно - фоновый шум. Вместо того чтобы полностью удалять конкретные частоты, мы можем:

Записать чистый фоновый шум отдельно (например, первые 3-5 секунды - это будет только шум, без речи);
Вычислить его спектральный профиль - среднюю амплитуду на каждой частоты;
Вычесть этот профиль из спектра исходного сигнала;
Применить маску, чтобы не удалить сам сигнал;

Предположим, что аудиосигнал состоит из двух частей:

x(n) = s(n) + w(n)

где:

$x(n)$ - наблюдаемый сигнал (речь + шум)
$s(n)$ - полезный сигнал (речь)
$w(n)$ - шум (фоновый)

В частотной области (после STFT):

|X(f,t)| = |S(f,t)| + |W(f,t)|

где $|X|, |S|, |W|$ - амплитуды спектра.

Оценка спектрального профиля шума
Сначала нам нужно понять, как выглядит шум на каждой частоте. Для этого:
1. Берём сегмент аудио, где есть только шум (в нашем случае начало голосового)
2. Вычисляем STFT этого сегмента, получая спектрограмму размера [частоты, время]
3. Усредняем по времени, получая профиль шума $P(f)$ :
$P(f) = \frac{1}{T} \sum_{t=1}^{T} |W(f,t)|$
где $T$ - количество временных кадров в сегменте шума.
Этот профиль показывает типичную амплитуду шума на каждой частоте.
Вычитание спектра с маской
Наивный подход - просто вычесть профиль из спектра:
$|S(f,t)| = |X(f,t)| - P(f)$
Но это создаёт проблемы:
- Может получиться отрицательное значение
- Можем удалить полезный сигнал
Поэтому используем мягкую маску.
Идея в том, что если амплитуда сигнала $|X(f,t)|$ намного больше профиля шума $P(f)$ , то это скорее всего полезный сигнал - трогать не нужно. Если амплитуды близки - это шум, нужно подавить.
Маска вычисляется по формуле:
$M(f,t) = \frac{1}{R} \left(1 - \frac{P(f) \cdot \theta}{|X(f,t)| + \epsilon}\right)$
где:
- $\theta$ (threshold) - пороговый уровень
- $R$ (reduction rate) - степень подавления шума
- $\epsilon = 10^{-12}$ - малое число для избежания деления на ноль
Это гиперпараметры метода, позволяющие задавать разные режимы работы денойзера.
Важно: маска не должна быть отрицательной!!!
Что делают параметры?
- Threshold ( $\theta$ ): Если увеличить, маска будет более агрессивно подавлять шум (но может задеть и сигнал)
- Reduction Rate ( $R$ ): Чем больше, тем мягче подавление. При $R=1$ подавление максимальное
Применение маски
Применяем маску к комплексному STFT (не только к амплитуде, но и к фазе):
$F'(f,t) = F(f,t) \cdot M(f,t)$
где $F(f,t)$ - комплексные значения STFT.
Это важно! Мы умножаем на маску весь комплексный спектр, а не только амплитуду. Это сохраняет фазовые соотношения.
Восстановление сигнала
Применяем обратное STFT (iSTFT) к отфильтрованному спектру $F'(f,t)$ , получая очищенный сигнал во временной области.

Задача 12 (6 баллов)

У вас есть класс Denoiser, который вам надо заполнить руководствуясь теорией. Тут нам множно пользоваться stft.

class Denoiser:
    def __init__(self, nfft=1024, winSize=1024, hopSize=512):
        super(Denoiser, self).__init__()
        self.nfft = nfft
        self.winSize = winSize
        self.hopSize = hopSize
        self.window = "hann"

    def fit(self, noiseSample):       
        _, _, spectrum = scipy.signal.stft(
            noiseSample,
            nfft=self.nfft,
            nperseg=self.winSize,
            noverlap=self.winSize - self.hopSize,
            window=self.window,
            return_onesided=True
        )
        self.profile = np.mean(np.abs(spectrum), axis=-1, keepdims=True)

    def __call__(self, audioWav, threshold=1, reductionRate=2, doPeakNormalize=True):     
        _, _, audioSpec = scipy.signal.stft(
            audioWav,
            nfft=self.nfft,
            nperseg=self.winSize,
            noverlap=self.winSize - self.hopSize,
            window=self.window,
            return_onesided=True
        )
     
        spg = np.abs(audioSpec)

        smol_value2 = 1e-12
        mask = np.clip((1 / reductionRate) * (1 - (self.profile * threshold) / (spg + smol_value2)), 0, 1) 

        audioSpec *= mask
        
        _, filteredAudio = scipy.signal.istft(
            audioSpec,
            nfft=self.nfft,
            nperseg=self.winSize,
            noverlap=self.winSize - self.hopSize,
            window=self.window,
            input_onesided=True
        )
        
        if len(filteredAudio) > len(audioWav):
            filteredAudio = filteredAudio[:len(audioWav)]
        
        if doPeakNormalize:
            max_filtered = np.max(np.abs(filteredAudio))
            max_original = np.max(np.abs(audioWav))
            if max_filtered > 1e-12:
                filteredAudio = filteredAudio / max_filtered * max_original
        
        return filteredAudio

Тут мы опять загрузим голосовую запись, которую можно скачать по ссылке. Но сейчас на фоне уже будет много шума. ОСТОРОЖНО, МОЖЕТ БЫТЬ ГРОМКО!

wav, sr = sf.read("./kitchenHood.wav")
wav = wav.mean(axis=-1)


print(f"Частота дискретизации: {sr}, Длительность: {wav.shape[-1] / sr} сек")
Audio(wav, rate=sr)

Для обучения будем использовать первые 5 секунд голосового. Дальше вам самостоятельно нужно будет понять, какие гиперпараметры лучше всего справятся с нашим шумом.

denoiser = Denoiser(nfft=1024, winSize=1024, hopSize=512)

noise_duration = 5
noise_samples = int(noise_duration * sr)
noise_segment = wav[:noise_samples]

denoiser.fit(noise_segment)

cleaned_wav = denoiser(wav, threshold=3, reductionRate=1, doPeakNormalize=True)

Далее вам необходим будет вывести и прослушать два голосовых, начальное и очищенное.

display(Audio(cleaned_wav, rate=sr))

Сейчас выведите 2 графика, на которых будет видно, что шум уменьшился, также можете посмотреть спектограмму шума, на котором вы обучались. В конце можно вывести 2 спектрограммы. Все графики надо проанализировать.

time = np.arange(len(wav)) / sr
plt.figure(figsize=(12, 4))

start = sr * 5
end = sr * 8

plt.plot(time[start:end], wav[start:end], label="Noisy signal")
plt.plot(time[start:end], cleaned_wav[start:end], label="Denoised signal")

plt.xlabel("Time [s]")
plt.ylabel("Amplitude")
plt.title("Noisy vs Denoised Signal")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()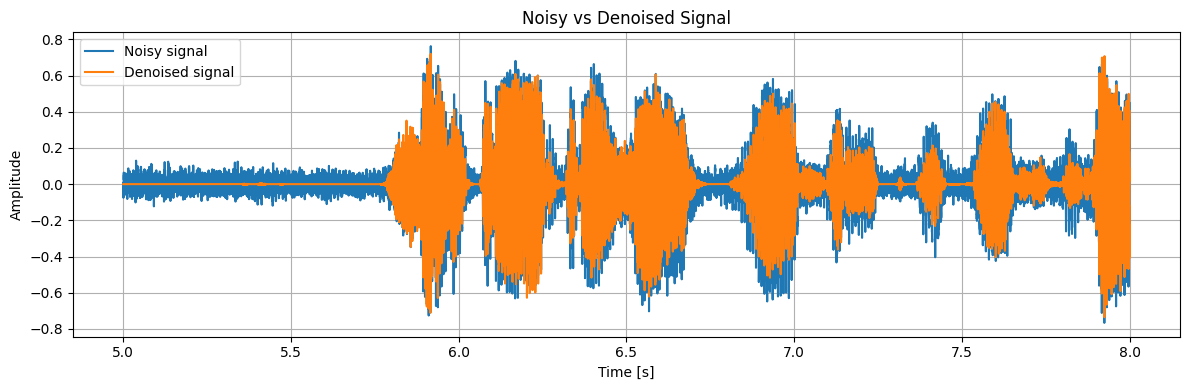

trans = STFTTransformer(nfft, winSize, hopSize, sr, windowType="hann")

plotSpectrogram(wav, trans)
plotSpectrogram(cleaned_wav, trans)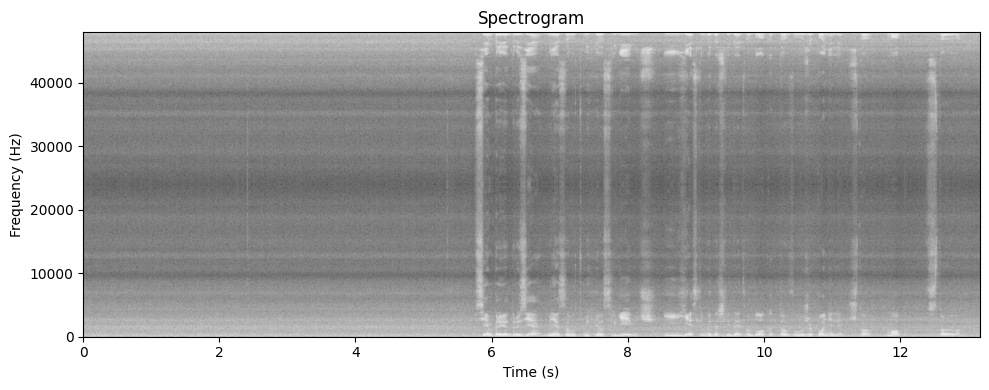

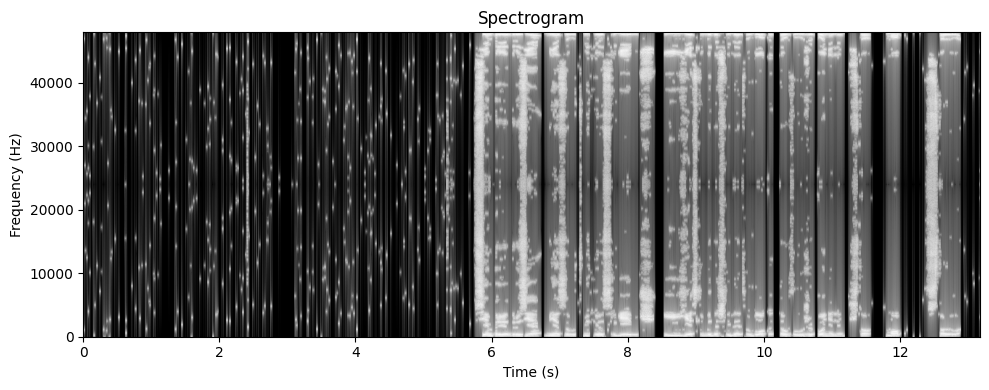
Объясните что произошло в первых 5 секундах и почему. Какие частоты исчезли? Слышны ли артефакты или странные звуки? Сохранилась ли речь?

In the first five seconds, there is just noise. Since we have, effectively, trained our denoiser on those five seconds, then the majority of waves in those five seconds have been nullified or reduced. Some black spots in the second spectrogram represent moments of silence when the speaker was not talking, but the noise was still present. Thus, it is clearly visible on the spectrogram.

Similarly, in the original spectrogram, there is smooth constant noise which after a five-second cutoff is interrupted by speech. Those unique soundwaves that are unlike noise soundwaves remain in the final spectrogram, especially that they have been present in the original one too. It can further be seen from the “voice message” graph that the amplitude of soundwaves was reduced by removing the noise.

The frequencies that disappeared are those that were present in those exact first five seconds. There are some artifacts present, but I tried to find such arguments that would make the final voice message sound as good as possible. Speech has, obviously, remained.

I find this unbelievably cool btw

Всем ЗВУУУУУУУУУК¶

Часть 3. Численное моделирование освещённости с использованием кратных интегралов¶

Эта часть лабораторной посвящена тому, как кратные интегралы позволяют рассчитывать освещённость поверхности с учётом расстояния и угла падения света. Мы будем моделировать разные типы источников, учитывать влияние материала поверхности, применять численные методы интегрирования и строить визуализации в виде тепловых карт и 3D-графиков.

Про списывание¶

Вчистую сгптшить не получится, у проверяющих зоркий глаз и отличная интуиция

Молния готов?

def start():
  return "О, да, Маквин готов!"

start()

'О, да, Маквин готов!'

Методы численного интегрирования [4 балла]¶

Когда мы считаем интеграл по области $D$ , мы как бы суммируем вклад каждой маленькой точки функции.

Существует множество методов вычислить интеграл в одномерном и многомерном случаях (Статья на вики). Для нашей цели (а конечная цель у нас вычислить уровень света и построить красоту) нам понадобятся три:

Метод прямоугольников
Метод трапеций
Метод Монте-Карло

Поговорим подробнее о каждом методе.

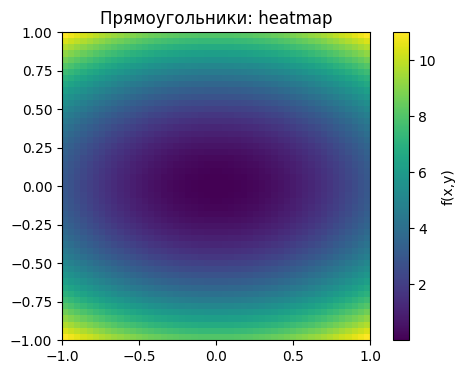
Метод прямоугольников¶

Идея:

Разбиваем область на маленькие квадраты.
Берём значение функции в центре каждого квадрата, умножаем на площадь квадрата, складываем все значения.

Простыми словами, чтобы посчитать освещенность, мы накрываем стол сеткой, берём яркость в центре каждого квадрата и суммируем.

Это очень просто и наглядно, но такой метод имеет очевидный минус: мы имеем очень грубое приближение, ошибка уменьшается как $O(1/n)$ (Что такое ошибка (с.37))

N = 50
x = np.linspace(-1,1,N)
y = np.linspace(-1,1,N)
X,Y = np.meshgrid(x,y)
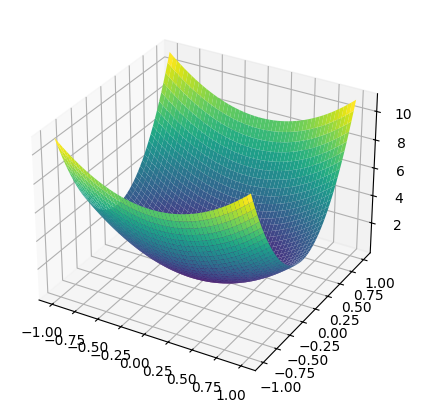
Z = X ** 2 + Y ** 2  # в качестве примера рассмотрим эту функцию

Вот как это будет выглядеть в 3D:

fig = plt.figure(figsize=(6,5))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
plt.show()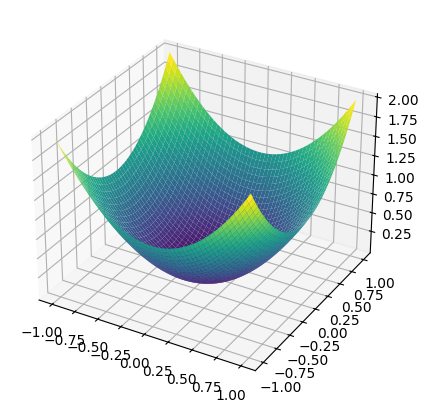

plt.imshow(Z, extent=[-1,1,-1,1], origin='lower', cmap='viridis')
plt.colorbar(label='f(x,y)')
plt.title('Прямоугольники: heatmap')
plt.show()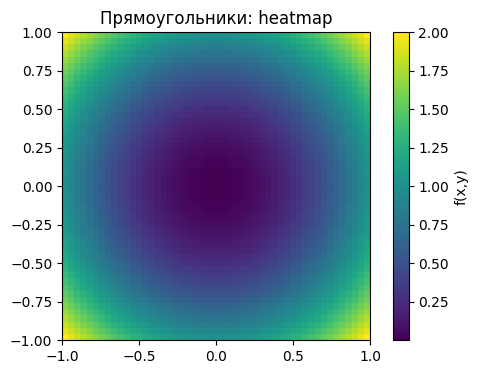

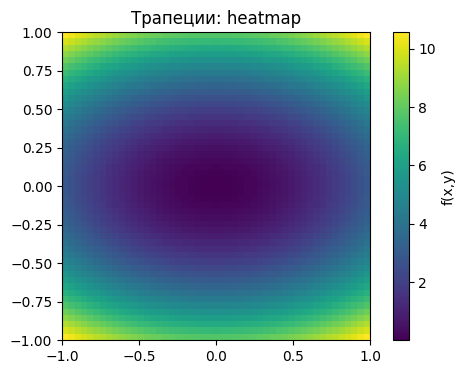
Метод трапеций¶

Идея:

Берём среднее значение функции по углам каждой ячейки.
Умножаем на площадь ячейки и суммируем.

Разница с методом прямоугольников в том, что если прямоугольники берут только центр, то трапеции «сглаживают» результат, учитывая углы.

Ошибка в этом случае уменьшается до $O(1/n^2)$

Z_trap = (Z[:-1,:-1] + Z[1:,:-1] + Z[:-1,1:] + Z[1:,1:])/4

plt.imshow(Z_trap, extent=[-1,1,-1,1], origin='lower', cmap='viridis')
plt.colorbar(label='f(x,y)')
plt.title('Трапеции: heatmap')
plt.show()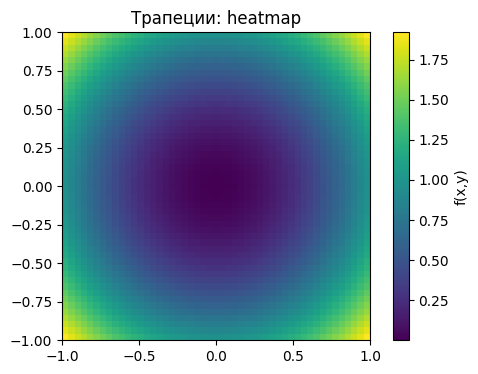

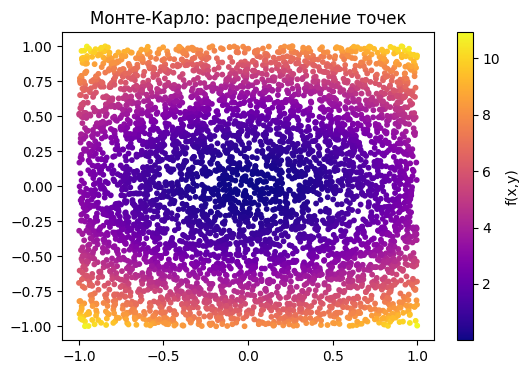
Метод Монте-Карло¶

Идея:

Случайно выбираем точки внутри области интегрирования, вычисляем среднее значение функции по этим точкам и умножаем его на площадь области.

Это удобно для сложной геометрии и многомерных задач, однако обладает высокой дисперсией результата и требует большого числа выборок для достижения высокой точности. Ошибка составляет $O(1/\sqrt{n})$

x_rand = np.random.uniform(-1,1,5000)
y_rand = np.random.uniform(-1,1,5000)
Z_rand = x_rand ** 2 + y_rand ** 2

plt.scatter(x_rand, y_rand, c=Z_rand, cmap='plasma', s=10)
plt.colorbar(label='f(x,y)')
plt.title('Монте-Карло: распределение точек')
plt.show()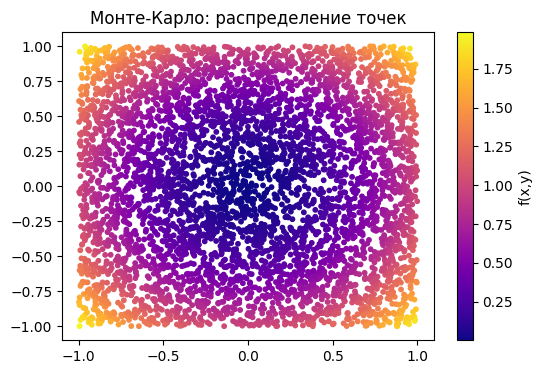

Посчитаем численные приближения интегралов:

dx = x[1] - x[0]
dy = y[1] - y[0]

res_rect = np.sum(Z) * dx * dy
res_trap = np.sum(Z_trap) * dx * dy
res_mc = np.mean(Z_rand) * 4

print("Прямоугольники:", res_rect)
print("Трапеции:", res_trap)
print("Монте-Карло:", res_mc)

Прямоугольники: 2.889952315786796
Трапеции: 2.6688879633486104
Монте-Карло: 2.642044458057318

Поскольку эти методы не вычисляют точное значение интеграла, а только пытаются его приблизить, то каждая из них, как говорилось выше, имеет ошибку, которая будет отличаться на разных функциях.

Задача 13.1 (0.5 балла)

Посчитайте ошибку для каждого из приближений:

from scipy.integrate import dblquad

result, _ = dblquad(lambda x, y: x ** 2 + y ** 2, -1, 1, lambda x: -1, lambda x: 1)

print("Actual value:", result)
print("Прямоугольники:", abs(res_rect - result))
print("Трапеции:", abs(res_trap - result))
print("Монте-Карло:", abs(res_mc - result))

Actual value: 2.6666666666666665
Прямоугольники: 0.22328564912012938
Трапеции: 0.0022212966819439295
Монте-Карло: 0.024622208609348384

Задача 13.2 (0.5 балла)

Сделайте выводы, почему получились именно такие результаты.

Approximating with rectangles is the coarsest approach, thus it is the least accurate, especially at a low number of squares. Depending on the way chosen points skew the function itself, we may get a wide range of errors, but for large enough squares, this approximation is least accurate, since the granularity is so relatively large.

Trapezoids approximate more accurately and are similar to approaches in modern 3d modelling software that approximate meshes using triangles. They wrap surfaces around much better since they may wrap around functions really well. With functions that change gradually and with reasonable granularity, this approach could work consistently great.

The Monte-Karlo approach has a huge level of dispersion, which makes it inconsistent. It may return different levels of accuracy depending on how lucky we were and whether points are distributed evenly. Additionally, in our examples it may often return a value less than the real values of the integral, which doesn’t typically happen with other approaches given that they approximate the functions with surface shapes from above. This method is sufficiently accurate in this case, but rerunning the code may yield a result that could be worse than the rectangle approximation approach, or even exceed the accuracy of trapezoids.

Задача 13.3 (3 балла)

Реализуйте три метода (прямоугольники, трапеции, Монте-Карло) для функций:

$f_1(x, y) = 3x + 8y$
$f_2(x, y) = \begin{cases}1\text{, если }3x^2 + 8y^2 < 0.5\\0\text{, иначе}\end{cases}$
$f_3(x, y) = 3x^2 + 8y^2$

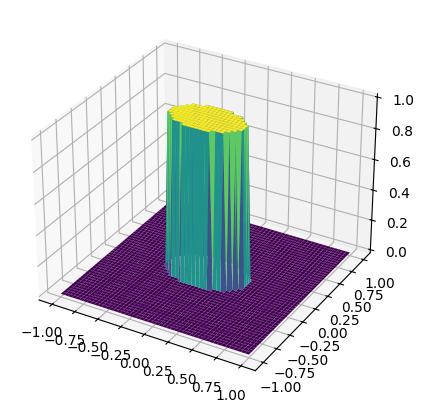
Постройте 2D heatmap и 3D surface для каждой функции, график ошибки vs N для каждого метода и сделайте выводы, какой метод удобнее для какой функции и почему.

functions = [lambda x, y: 3 * x + 8 * y, 
             lambda x, y: np.where(3 * x ** 2 + 8 * y ** 2 < 0.5, 1, 0), 
             lambda x, y: 3 * x ** 2 + 8 * y ** 2]

for func in functions:
    N = 50
    x = np.linspace(-1,1,N)
    y = np.linspace(-1,1,N)
    X,Y = np.meshgrid(x,y)
    Z = func(X, Y)

    fig = plt.figure(figsize=(6,5))
    ax = fig.add_subplot(111, projection='3d')
    ax.plot_surface(X, Y, Z, cmap='viridis')
    plt.show()

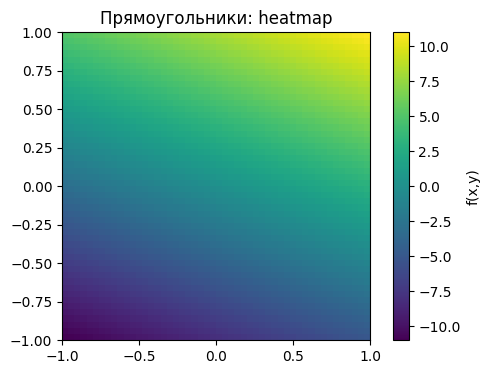
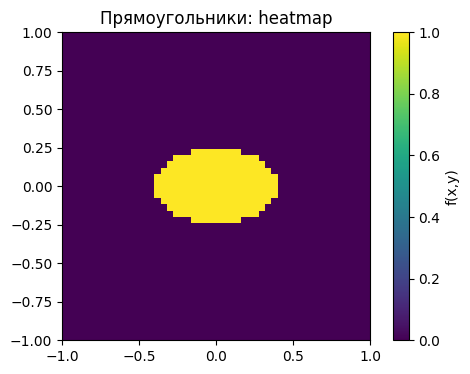
    plt.imshow(Z, extent=[-1,1,-1,1], origin='lower', cmap='viridis')
    plt.colorbar(label='f(x,y)')
    plt.title('Прямоугольники: heatmap')
    plt.show()

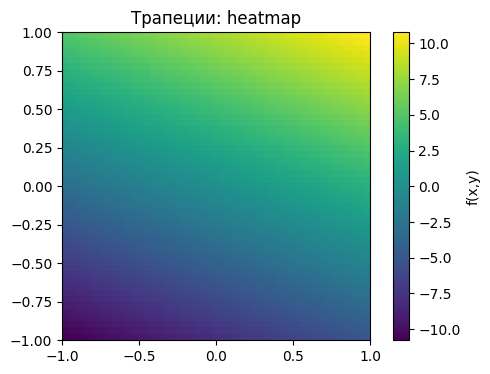
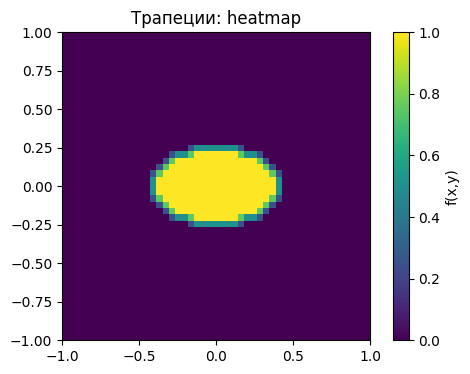
    Z_trap = (Z[:-1,:-1] + Z[1:,:-1] + Z[:-1,1:] + Z[1:,1:])/4

    plt.imshow(Z_trap, extent=[-1,1,-1,1], origin='lower', cmap='viridis')
    plt.colorbar(label='f(x,y)')
    plt.title('Трапеции: heatmap')
    plt.show()

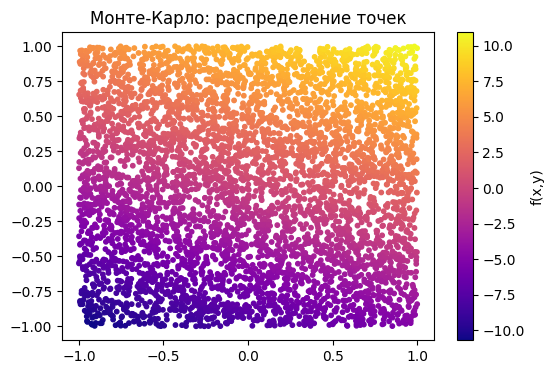
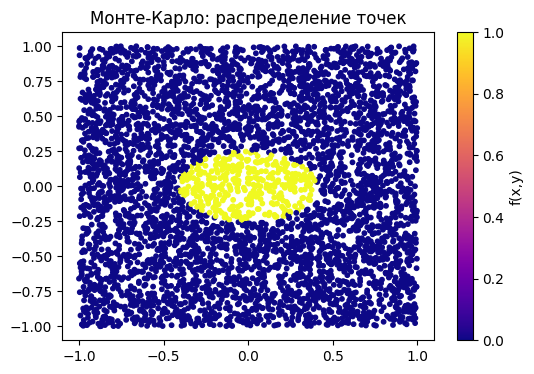
    x_rand = np.random.uniform(-1,1,5000)
    y_rand = np.random.uniform(-1,1,5000)
    Z_rand = func(x_rand, y_rand)

    plt.scatter(x_rand, y_rand, c=Z_rand, cmap='plasma', s=10)
    plt.colorbar(label='f(x,y)')
    plt.title('Монте-Карло: распределение точек')
    plt.show()

    dx = x[1] - x[0]
    dy = y[1] - y[0]

    res_rect = np.sum(Z) * dx * dy
    res_trap = np.sum(Z_trap) * dx * dy
    res_mc = np.mean(Z_rand) * 4

    print("Прямоугольники:", res_rect)
    print("Трапеции:", res_trap)
    print("Монте-Карло:", res_mc)

    result, _ = dblquad(func, -1, 1, lambda x: -1, lambda x: 1)

    print("Actual value:", result)
    print("Прямоугольники:", abs(res_rect - result))
    print("Трапеции:", abs(res_trap - result))
    print("Монте-Карло:", abs(res_mc - result))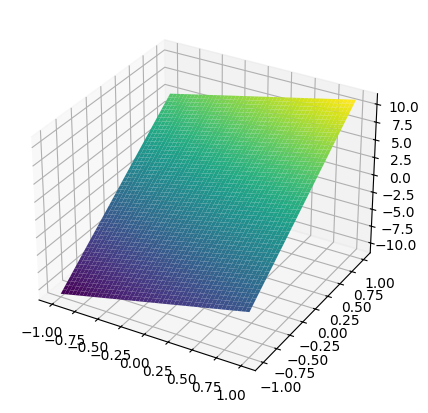

Прямоугольники: -3.0303863449327123e-15
Трапеции: -1.5151931724663562e-15
Монте-Карло: 0.189800868165033
Actual value: 0.0
Прямоугольники: 3.0303863449327123e-15
Трапеции: 1.5151931724663562e-15
Монте-Карло: 0.189800868165033

Прямоугольники: 0.3198667221990844
Трапеции: 0.3198667221990844
Монте-Карло: 0.2912

c:\Users\artemis\AppData\Local\Programs\Python\Python312\Lib\site-packages\scipy\integrate\_quadpack_py.py:1272: IntegrationWarning: The maximum number of subdivisions (50) has been achieved.
  If increasing the limit yields no improvement it is advised to analyze 
  the integrand in order to determine the difficulties.  If the position of a 
  local difficulty can be determined (singularity, discontinuity) one will 
  probably gain from splitting up the interval and calling the integrator 
  on the subranges.  Perhaps a special-purpose integrator should be used.
  quad_r = quad(f, low, high, args=args, full_output=self.full_output,

Actual value: 0.3206029177867963
Прямоугольники: 0.0007361955877118742
Трапеции: 0.0007361955877118742
Монте-Карло: 0.029402917786796268

Прямоугольники: 15.894737736827373
Трапеции: 14.67888379841736
Монте-Карло: 14.378898332854535
Actual value: 14.666666666666668
Прямоугольники: 1.2280710701607056
Трапеции: 0.012217131750691834
Монте-Карло: 0.2877683338121333

functions = [lambda x, y: 3 * x + 8 * y, 
             lambda x, y: np.where(3 * x ** 2 + 8 * y ** 2 < 0.5, 1, 0), 
             lambda x, y: 3 * x ** 2 + 8 * y ** 2]

errors = {}
for func in functions:
    h = hash(func)
    errors[h] = {"rect": [],
                  "trap": [],
                  "mc": []}
    
    result, _ = dblquad(func, -1, 1, lambda x: -1, lambda x: 1)
    for N in range(10, 101):
        x = np.linspace(-1,1,N)
        y = np.linspace(-1,1,N)
        X,Y = np.meshgrid(x,y)
        Z = func(X, Y)

        Z_trap = (Z[:-1,:-1] + Z[1:,:-1] + Z[:-1,1:] + Z[1:,1:])/4

        x_rand = np.random.uniform(-1,1,5000)
        y_rand = np.random.uniform(-1,1,5000)
        Z_rand = func(x_rand, y_rand)

        dx = x[1] - x[0]
        dy = y[1] - y[0]

        res_rect = np.sum(Z) * dx * dy
        res_trap = np.sum(Z_trap) * dx * dy
        res_mc = np.mean(Z_rand) * 4

        errors[h]["rect"].append(abs(res_rect - result))
        errors[h]["trap"].append(abs(res_trap - result))
        errors[h]["mc"].append(abs(res_mc - result))

c:\Users\artemis\AppData\Local\Programs\Python\Python312\Lib\site-packages\scipy\integrate\_quadpack_py.py:1272: IntegrationWarning: The maximum number of subdivisions (50) has been achieved.
  If increasing the limit yields no improvement it is advised to analyze 
  the integrand in order to determine the difficulties.  If the position of a 
  local difficulty can be determined (singularity, discontinuity) one will 
  probably gain from splitting up the interval and calling the integrator 
  on the subranges.  Perhaps a special-purpose integrator should be used.
  quad_r = quad(f, low, high, args=args, full_output=self.full_output,

for key in errors:
    for type in ["rect", "trap", "mc"]:
        plt.plot(
          np.array(range(10, 101)),
          errors[key][type],
          label=type
        )

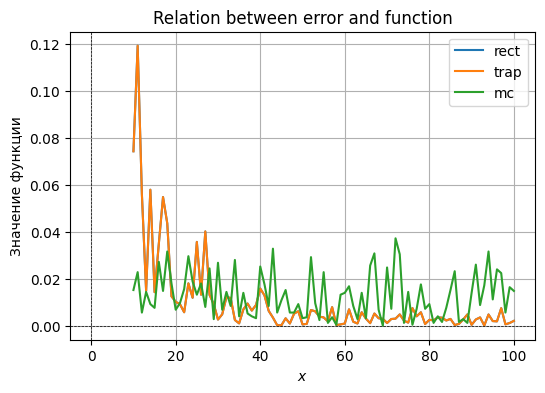
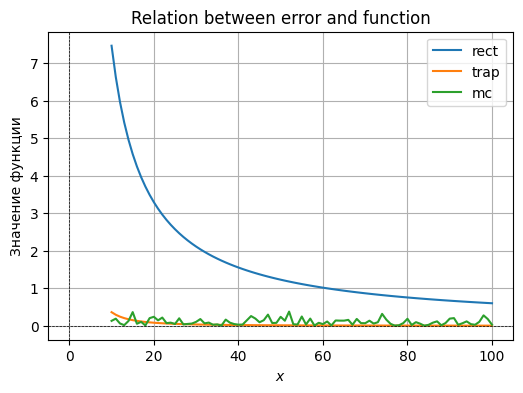
    plt.title(f'Relation between error and function')
    plt.xlabel('$x$')
    plt.ylabel('Значение функции')
    plt.axhline(0, color='black', linewidth=0.5, ls='--')
    plt.axvline(0, color='black', linewidth=0.5, ls='--')
    plt.grid()
    plt.legend()

    plt.show()

for key in errors:
    print(errors[key]["rect"])
    print(errors[key]["trap"])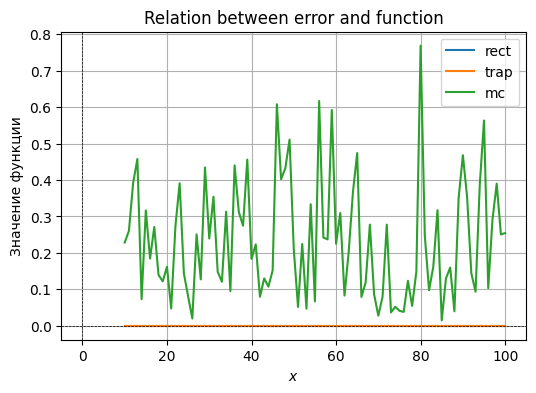

[2.280754460464519e-15, 2.7711166694643892e-15, 3.758242569309623e-15, 1.5789838572446664e-15, 5.3816254542776825e-15, 2.3201395453391005e-15, 0.0, 0.0, 1.5735202452818834e-15, 2.8070824128794107e-15, 1.2596879525940832e-15, 2.2737367544323195e-15, 3.0935193937854697e-15, 0.0, 1.7192716479639452e-15, 0.0, 1.4551915228366837e-15, 4.036219090708256e-15, 1.247592183501959e-15, 2.3201395453391005e-15, 2.1628887081401403e-15, 1.0105496686365865e-15, 0.0, 0.0, 3.340660061608546e-15, 0.0, 0.0, 4.210623619319116e-15, 2.6573986903518726e-15, 2.5193759051881613e-15, 3.587750302851794e-15, 1.1368683772161623e-15, 3.2462630640318735e-15, 1.0311731312618256e-15, 1.9675385652199615e-15, 0.0, 1.7965327442428173e-15, 0.0, 1.6468894554512017e-15, 6.315935428978657e-15, 3.0303863449327123e-15, 2.9103830456733756e-15, 0.0, 1.3454063635694187e-15, 2.5902305497270997e-15, 2.4951843670039107e-15, 2.405275244358159e-15, 2.3201395453391005e-15, 2.2394452490561482e-15, 0.0, 1.0450958940223261e-15, 1.0105496686365865e-15, 9.77688472747036e-16, 9.464044763506e-16, 0.0, 0.0, 3.4442402907377168e-15, 3.340660061608546e-15, 0.0, 0.0, 0.0, 1.4848893090170267e-15, 2.8867120072142063e-15, 1.4035412064397054e-15, 1.3653514006724386e-15, 1.3286993451759308e-15, 2.587007151709653e-15, 2.5193759051881613e-15, 3.6815437413645286e-15, 1.1959167676172645e-15, 1.1658320163729273e-15, 3.410605131648487e-15, 1.108970829779519e-15, 1.0820876880106244e-15, 2.112340721202905e-15, 2.062346262523651e-15, 0.0, 9.837692826099853e-16, 1.9225677405690074e-15, 9.395606423274035e-16, 1.8371310728906606e-15, 1.3473995581821198e-15, 3.5145309089160477e-15, 2.578907471945918e-15, 3.3649936936910222e-15, 1.2351670915884078e-15, 1.6124005793204198e-15, 3.1579677144893454e-15, 1.5465953053849404e-15, 3.7879829311658906e-15, 2.9694756103187182e-15]
[2.3684757858670005e-15, 2.3447910280083295e-15, 1.5855085839274973e-15, 0.0, 2.6908127271388413e-15, 2.3201395453391005e-15, 0.0, 0.0, 1.5735202452818834e-15, 2.8070824128794107e-15, 3.77906385778225e-15, 3.410605131648479e-15, 2.0623462625236465e-15, 2.8186819269822177e-15, 0.0, 1.5789838572446686e-15, 0.0, 1.3454063635694187e-15, 1.247592183501959e-15, 2.3201395453391005e-15, 0.0, 0.0, 1.8928089527012e-15, 0.0, 0.0, 0.0, 1.4848893090170267e-15, 1.4035412064397054e-15, 1.3286993451759363e-15, 1.2596879525940807e-15, 1.1959167676172645e-15, 2.2737367544323246e-15, 0.0, 4.124692525047302e-15, 9.837692826099808e-16, 9.395606423274035e-16, 8.982663721214087e-16, 0.0, 0.0, 0.0, 1.5151931724663562e-15, 0.0, 1.3986846624727827e-15, 2.6908127271388373e-15, 2.5902305497270997e-15, 3.742776550505866e-15, 2.405275244358159e-15, 3.4802093180086507e-15, 3.359167873584222e-15, 1.0814443540700666e-15, 0.0, 1.0105496686365865e-15, 9.77688472747036e-16, 9.464044763506e-16, 3.666393355597594e-15, 0.0, 0.0, 3.340660061608546e-15, 0.0, 0.0, 0.0, 1.4848893090170267e-15, 0.0, 2.8070824128794107e-15, 1.3653514006724386e-15, 1.3286993451759308e-15, 1.2935035758548264e-15, 3.779063857782242e-15, 2.454362494243019e-15, 2.391833535234529e-15, 1.1658320163729273e-15, 2.2737367544323246e-15, 4.435883319118076e-15, 2.1641753760212487e-15, 3.1685110818043573e-15, 3.093519393785477e-15, 2.0141059139608144e-15, 9.837692826099853e-16, 0.0, 0.0, 1.8371310728906606e-15, 3.593065488485653e-15, 2.1416672726207167e-15, 1.7192716479639452e-15, 2.103121058556889e-15, 8.234447277256051e-16, 1.2093004344903149e-15, 1.5789838572446727e-15, 2.319892958077411e-15, 3.7879829311658906e-15, 3.711844512898398e-15]
[0.07445881060826542, 0.1193970822132035, 0.056140107869440736, 0.015047362231240868, 0.05809530706527477, 0.014480468807204716, 0.03495263776875912, 0.05497791778679628, 0.043786308790256356, 0.012730415546537366, 0.010353610307571925, 0.009397082213203567, 0.005927694458101651, 0.018240057419815492, 0.012100295823789298, 0.035880695564573795, 0.013402917786796587, 0.04034382777533341, 0.01333268459063719, 0.00937842799087818, 0.002821576862431119, 0.0050473622312408595, 0.012383554637760863, 0.012009167786796282, 0.002629405445526367, 0.001196390171681383, 0.007133530031694035, 0.009643995793450932, 0.006643247297206667, 0.009036971409878913, 0.01601772652615624, 0.013102917786795731, 0.006504167043190734, 0.003660120761957264, 0.0004298512643520769, 0.00035498390249932843, 0.0033476994971536334, 0.001132218353904424, 0.005336421280654258, 0.006366806675685732, 0.0007361955877118742, 0.00099708221320427, 0.006877427590718299, 0.006320159136280201, 0.004067783530398328, 0.00373048980325813, 0.0020417103123774316, 0.00810291778679656, 0.000504425943152087, 0.000745605063848187, 0.0011437067463842543, 0.00717485999098133, 0.0018910354515812022, 0.0011440208044867228, 0.005927694458101651, 0.003220105286796282, 0.0012905733374640738, 0.005384226382165458, 0.0033830469915194783, 0.003128869343889562, 0.0013422582614860956, 0.0030518973786328174, 0.0032055759895346925, 0.005016498033709571, 0.0023443326864022174, 0.0015300259677678008, 0.007714028897908565, 0.004189325980516023, 0.005927694458101929, 0.000896096019910364, 0.002705144993974007, 0.0024779177867956803, 0.003737883920260532, 0.0036088609163571483, 0.0024145014709313073, 0.0030932273379210007, 0.0005043486491906335, 0.0009706841469898642, 0.002821576862430064, 0.0050037442330778115, 0.0005686514595125702, 0.002853872336661456, 0.003732974543225742, 0.00028555102227700857, 0.004983855250548508, 0.002167566595278003, 0.0020563619915956455, 0.007668890009017382, 0.0007914918210271682, 0.0013462700516050918, 0.0022680539973864433]
[0.07445881060826542, 0.1193970822132035, 0.056140107869440736, 0.015047362231240868, 0.05809530706527477, 0.014480468807204716, 0.03495263776875912, 0.05497791778679628, 0.043786308790256356, 0.012730415546537366, 0.010353610307571925, 0.009397082213203567, 0.005927694458101651, 0.018240057419815492, 0.012100295823789298, 0.035880695564573795, 0.013402917786796587, 0.04034382777533341, 0.01333268459063719, 0.00937842799087818, 0.002821576862431119, 0.0050473622312408595, 0.012383554637760863, 0.012009167786796282, 0.002629405445526367, 0.001196390171681383, 0.007133530031694035, 0.009643995793450932, 0.006643247297206667, 0.009036971409878913, 0.01601772652615624, 0.013102917786795731, 0.006504167043190734, 0.003660120761957264, 0.0004298512643520769, 0.00035498390249932843, 0.0033476994971536334, 0.001132218353904424, 0.005336421280654258, 0.006366806675685732, 0.0007361955877118742, 0.00099708221320427, 0.006877427590718299, 0.006320159136280201, 0.004067783530398328, 0.00373048980325813, 0.0020417103123774316, 0.00810291778679656, 0.000504425943152087, 0.000745605063848187, 0.0011437067463842543, 0.00717485999098133, 0.0018910354515812022, 0.0011440208044867228, 0.005927694458101651, 0.003220105286796282, 0.0012905733374640738, 0.005384226382165458, 0.0033830469915194783, 0.003128869343889562, 0.0013422582614860956, 0.0030518973786328174, 0.0032055759895346925, 0.005016498033709571, 0.0023443326864022174, 0.0015300259677678008, 0.007714028897908565, 0.004189325980516023, 0.005927694458101929, 0.000896096019910364, 0.002705144993974007, 0.0024779177867956803, 0.003737883920260532, 0.0036088609163571483, 0.0024145014709313073, 0.0030932273379210007, 0.0005043486491906335, 0.0009706841469898642, 0.002821576862430064, 0.0050037442330778115, 0.0005686514595125702, 0.002853872336661456, 0.003732974543225742, 0.00028555102227700857, 0.004983855250548508, 0.002167566595278003, 0.0020563619915956455, 0.007668890009017382, 0.0007914918210271682, 0.0013462700516050918, 0.0022680539973864433]
[7.464106081390025, 6.629333333333324, 5.961432506887064, 5.415123456790113, 4.960097102108939, 4.575315840621943, 4.245728395061715, 3.960286458333332, 3.710699504715386, 3.490626428898043, 3.2951353452884256, 3.120333333333324, 2.9631069358960467, 2.820936639118468, 2.6917618695377925, 2.5738811728395206, 2.4658773333333137, 2.3665604612349966, 2.274924215482052, 2.190111758989289, 2.111389014173067, 2.0381234567901174, 1.9697671556286274, 1.9058430989583321, 1.8459340883583053, 1.789673654929107, 1.7367385811467528, 1.6868427069044465, 1.6397317697536877, 1.5951790834426411, 1.5529819001219636, 1.512958333333362, 1.4749447434986251, 1.4387935068207511, 1.4043711035925348, 1.3715564738291732, 1.3402395976222792, 1.3103202651981878, 1.2817070077599624, 1.2543161651234236, 1.2280710701607056, 1.2029013333333598, 1.1787422132764185, 1.1555340615991323, 1.1332218318925378, 1.11175464444778, 1.0910853994490424, 1.0711704324586808, 1.0519692068994644, 1.0334440389792814, 1.0155598511370219, 0.9982839506172763, 0.9815858302383962, 0.9654369887997234, 0.9498107689087725, 0.9346822102864571, 0.9200279168563217, 0.905825936128938, 0.8920556495756617, 0.8786976728407687, 0.8657337647776444, 0.8531467444120562, 0.8409204150379637, 0.8290394947416662, 0.8174895527273396, 0.8062569508880078, 0.7953287901233974, 0.7846928609612291, 0.7743375980852907, 0.7642520384137974, 0.7544257824093972, 0.7448489583333622, 0.7355121891862524, 0.7264065621025306, 0.7175235999885281, 0.7088552352158075, 0.7003937851957733, 0.6921319296833932, 0.6840626896662698, 0.6761794077134713, 0.6684757296657278, 0.6609455875629138, 0.6535831837124437, 0.6463829758088586, 0.639339663026881, 0.6324481730124418, 0.6257036497059154, 0.6191014419367793, 0.6126370927302354, 0.6063063292789277, 0.6001050535282051]
[0.3621399176954654, 0.2933333333333277, 0.24242424242425464, 0.2037037037036935, 0.17357001972386676, 0.14965986394556374, 0.1303703703703647, 0.11458333333333215, 0.10149942329873696, 0.09053497942387878, 0.08125577100646098, 0.07333333333332703, 0.06651549508691801, 0.060606060606069434, 0.05545053560174473, 0.050925925925936255, 0.046933333333317506, 0.04339250493094582, 0.04023776863282613, 0.03741496598638072, 0.03487911216806516, 0.03259259259258407, 0.03052375997222434, 0.02864583333333215, 0.02693602693599928, 0.025374855824686904, 0.0239455782313005, 0.022633744855975024, 0.021426832237644078, 0.020313942751579717, 0.01928555774711782, 0.018333333333361068, 0.017449930596894703, 0.016628873771757924, 0.015864431224065, 0.01515151515148716, 0.014485596707787707, 0.013862633900421528, 0.013279010110121447, 0.012731481481452533, 0.012217131750691834, 0.011733333333358686, 0.011277713699838543, 0.010848126232723132, 0.010442624896159103, 0.010059442158160792, 0.009696969696978641, 0.009353741496580525, 0.009028419000713939, 0.008719778041973214, 0.008426697309220188, 0.008148148148139356, 0.007883185523635206, 0.0076309399930334365, 0.007390610565208178, 0.007161458333332149, 0.006942800788955594, 0.006734006733982056, 0.006534491720476154, 0.006343713956175279, 0.006161170622434042, 0.005986394557828234, 0.005818951266242323, 0.005658436214000417, 0.0055044723838086895, 0.005356708059350623, 0.00521481481476016, 0.005078485687869616, 0.0049474335188719465, 0.004821389436793666, 0.004700101479489405, 0.004583333333359363, 0.004470863181422757, 0.004362482649241883, 0.004257995838740314, 0.004157218442962574, 0.004059976931980458, 0.003966107806069985, 0.0038754569075223344, 0.00378787878785225, 0.0037032361234548006, 0.003621399176997997, 0.0035422453005349297, 0.003465658475089839, 0.003391528885780204, 0.003319752527580988, 0.00325023084019449, 0.0031828703704199768, 0.003117582456566126, 0.0030542829376916103, 0.0029928918818065142]

Conclusions:

Fair to say that the Monte-Carlo methods basically does not depend on sufficiently large $N$ after some point, since choosing higher granularity does not outweigh the randomness of the distribution.

Function $f_1(x, y) = 3x+8y$ is a linear combination, so it describes a plane in 3D space. Approximating such function with flat shapes, such as rectangles or trapezoids yields a negligible error value, which is sometimes even treated as exact zero by python, given it’s so small.

Randomly choosing points to approximate this function would not work out well and given a large error value. There is a much better way geometrically that yields near-exact results. Thus, the rectangular and the trapezoidal approximations are optimal.

Choosing different $N$ has basically no effect because our function is uniform and flat, and the values approximated do not seem to depend on them.
Function $f_2(x,y)$ is an indicator function that returns true if a value is within a certain region and false otherwise. For this function, rectangles and trapezoids are absolutely identical because the surfaces are flat (parallel to oXY), yielding the same shapes, which give us a steadily decreasing function as $N$ grows.

Taking random points appears to be more precise for smaller values of $N$ , but as $N$ increases, rectangular and trapezoidal approximations overtake it since the error value on the boundary of the elliptical shape contribute less and less to the overall value.
Approximating a more sophisticated function $f_3(x, y)=3x^2+8y^2$ with rectangles works terribly, as we have figured out in one of the previous tasks, whereas the comparison between trapezoids and the MC method behaves similarly to point 2 directly above (for small N, MC is better, which is eventually overtaken by trapezoids as N increases).

Точечный источник света [5 баллов]¶

Теперь непосредственно обратимся к свету :)

Представьте лампочку над столом. Каждая маленькая частица света падает на поверхность. Чем ближе точка на столе к лампочке, тем свет ярче. Чем угол падения острее — тем слабее свет. Это называется закон Ламберта (статья на вики).

Формула интенсивности в точке $P(x, y, 0)$ , если источник в $S(x_S, y_S, z_S)$ :

L(x, y) = \frac{\cos{\theta}}{r^2}, r = \sqrt{(x-x_s)^2+(y-y_s)^2+(z-z^s)^2}, \cos{θ} = \frac{z_s}{r}

И упрощаем:

L(x,y) = \frac{z_s}{r^3}

Чтобы найти общее освещение поверхности, нужно разбить поверхность на крошечные кусочки, для каждого посчитать вклад света и сложить все вклады, поэтому мы используем кратный интеграл:

E = \iint\limits_D L(x, y)dxdy

Теперь используем всё это. Мы можем задавать параметры нашего точечного источника:

# Сетка
N = 100
x = np.linspace(-1, 1, N)
y = np.linspace(-1, 1, N)
X, Y = np.meshgrid(x, y)

# Точечный источник
xs, ys, zs = 0, 0, 1.5
L_point = zs / ((X - xs)**2 + (Y - ys)**2 + zs**2)**(3/2)

Мы можем вычислить освещенность в конкретных точках:

test_points = [(0,0), (0.5,0.5), (-0.7,0)]
print("Освещённость в точках:")
for (px, py) in test_points:
    val = zs / ((px-xs)**2 + (py-ys)**2 + zs**2)**(3/2)
    print(f"L({px}, {py}) = {val:.5f}")

Освещённость в точках:
L(0, 0) = 0.44444
L(0.5, 0.5) = 0.32892
L(-0.7, 0) = 0.33072

И нарисовать:

# 2D
plt.figure(figsize=(6,5))
plt.imshow(L_point, extent=[-1,1,-1,1], origin='lower', cmap='inferno', norm=LogNorm())
plt.colorbar(label='L(x,y)')
plt.title('Точечный источник: 2D Heatmap')
plt.show()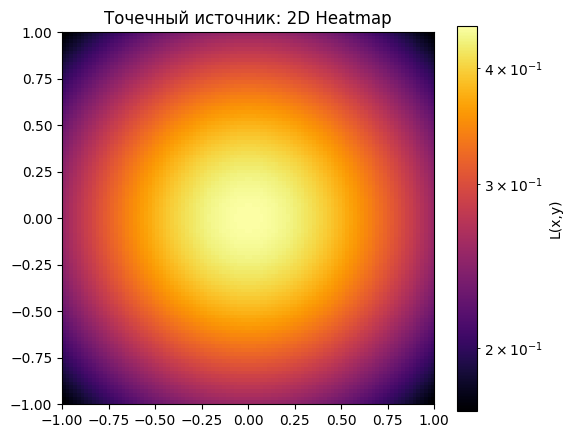

# 3D
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, L_point, cmap='inferno', linewidth=0, antialiased=True)
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('L(x,y)')
ax.set_title('Точечный источник: 3D Surface')
plt.show()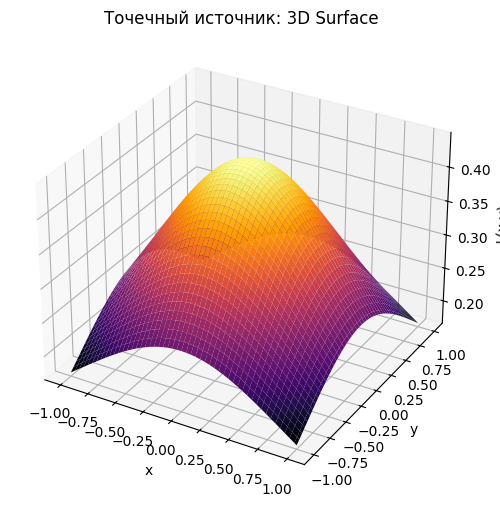

Задача 14.1 (2.5 балла)

Рассмотрим два точечных источника в точках $S_1(x_1, y_1, z_1) = (-0.5, 0.5, 1.5)$ , $S_2(x_2, y_2, z_2) = (0.5, -0.5, 1)$ . Теперь освещенность в точке $P(x, y, 0)$ задается как сумма двух источников:

L(x, y) = \frac{z_1}{((x-x_1)^2 + (y-y_1)^2 + z_1^2)^\frac32} + \frac{z_2}{((x-x_2)^2 + (y-y_2)^2 + z_2^2)^\frac32}

Реализуйте расчет освещенности на сетке $x, y \in [-1, 1], N = 50$ . Постройте графики в 2D и 3D. Реализуйте три метода интегрирования (из прошлого раздела) для суммарной освещённости $E = \int\int_D L(x, y)dxdy$ . Проведите анализ зависимости интеграла от числа точек $N$ (например, 10, 20, 50, 100).

S_1 = (-0.5, -0.5, 1.5)
S_2 = (0.5, -0.5, 1)

def enlightenment(X, Y, xs, ys, zs):
    return zs / ((X - xs)**2 + (Y - ys)**2 + zs**2)**(3/2)

N = 50
x = np.linspace(-1, 1, N)
y = np.linspace(-1, 1, N)
X, Y = np.meshgrid(x, y)

L_point = enlightenment(X, Y, *S_1) + enlightenment(X, Y, *S_2)

# 2D
plt.figure(figsize=(6,5))
plt.imshow(L_point, extent=[-1,1,-1,1], origin='lower', cmap='inferno', norm=LogNorm())
plt.colorbar(label='L(x,y)')
plt.title('Точечный источник: 2D Heatmap')
plt.show()

# 3D
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, L_point, cmap='inferno', linewidth=0, antialiased=True)
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('L(x,y)')
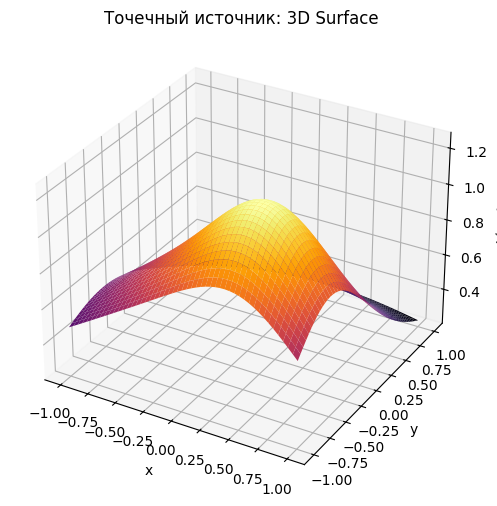
ax.set_title('Точечный источник: 3D Surface')
plt.show()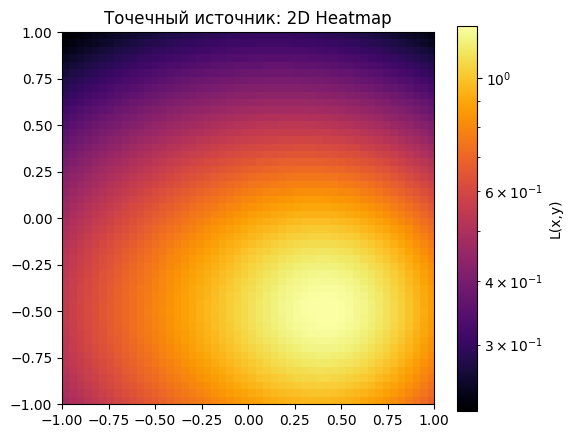

values = {"rect": [],
          "trap": [],
          "mc": []}

func = lambda x, y: enlightenment(x, y, *S_1) + enlightenment(x, y, *S_2)
R = range(10, 101)

for N in R:
    x = np.linspace(-1,1,N)
    y = np.linspace(-1,1,N)
    X,Y = np.meshgrid(x,y)
    Z = func(X, Y)

    Z_trap = (Z[:-1,:-1] + Z[1:,:-1] + Z[:-1,1:] + Z[1:,1:])/4

    x_rand = np.random.uniform(-1,1,5000)
    y_rand = np.random.uniform(-1,1,5000)
    Z_rand = func(x_rand, y_rand)

    dx = x[1] - x[0]
    dy = y[1] - y[0]

    res_rect = np.sum(Z) * dx * dy
    res_trap = np.sum(Z_trap) * dx * dy
    res_mc = np.mean(Z_rand) * 4

    values["rect"].append(res_rect)
    values["trap"].append(res_trap)
    values["mc"].append(res_mc)

for type in ["rect", "trap", "mc"]:
    plt.plot(
      np.array(R),
      values[type],
      label=type
    )

plt.title(f'Integral values relation')
plt.xlabel('$x$')
plt.ylabel('Function value')
plt.axhline(0, color='black', linewidth=0.5, ls='--')
plt.axvline(0, color='black', linewidth=0.5, ls='--')
plt.grid()
plt.ylim(2.5, 3.5)
plt.legend()

plt.show()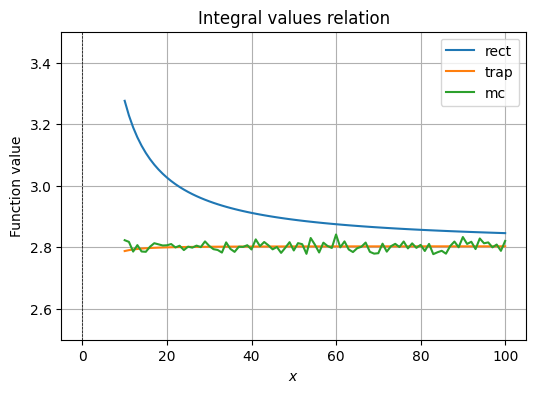

The behavior of the values by integration method is same as in the analysis we have done for different ways of calculating integrals and their errors. We may observe that rectangular approximation for a sophisticated function is garbage, MC approximation is inconsistent, but follows the actual value, whereas the trapezoid approximation quickly becomes accurate at a small value of $N$ .

Задача 14.2 (0.5 балла)

В задании вы интегрировали тремя методами. Сделайте выводы, какой метод работает лучше и почему? Всегда ли он будет оптимальным?

Trapezoid approach for approximating meshes of polynomial surfaces would always work better because for a sufficiently large $N$ , we can follow the surface very closely. As functions increase in complexity, this method wins without sacrificing much computational power, as well as being deterministic.

Теперь поговорим о том, как найти точку наибольшей освещенности. Логично, что ответ зависит от числа источников:

Для одного точечного источника на плоскости $z = 0$ функция $L(x, y) = \frac{z_1}{((x-x_s)^2 + (y-y_s)^2 + z_s^2)^\frac32}$ монотонно убывает при удалении от проекции источника $(x_s, y_s)$ . Значит максимум достигается в точке проекции $(x, y) = (x_s, y_s)$ (если она лежит в рассматриваемой области). Если проекция вне области — максимум будет на ближайшей к ней точке области (граница).
Для двух и более источников $L(x, y) = ∑_iL_i(x, y)$ аналитического простого решения обычно нет: максимум найден там, где сумма каждого вклада наиболее велика — это задача оптимизации функции двух переменных.

В целом это можно запрогать одним из двух подходов:

Сначала быстро найти приближённый максимум на относительно грубой равномерной сетке, затем «зумить» вокруг лучшей точки и повторять — каждый раз делая сетку плотнее в локальной окрестности. Метод стабилен, нечувствителен к локальным особенностям (даёт глобально хорошее начало) и прост в реализации.
Идея: взять несколько хороших стартов (например, вершины грубой сетки или случайные стартовые точки), запустить локальную оптимизацию для каждого старта, и выбрать лучший результат. Это быстрее и даёт высокую точность, но требует аккуратности (локальные минимумы/максимумы) и scipy.optimize.

Задача 14.3 (2 балла)

Любым из двух способов найдите точку максимальной освещенности для заданных в Задаче 14.1 параметров

from scipy.optimize import minimize

x, y = minimize(
    lambda xy: -func(xy[0], xy[1]),
    [-0.5, 0.5],
    bounds=[(-1,1), (-1,1)]
).x
z = func(x, y)

display(Latex(f"The point with the maximum light value would be $\\approx A({round(x, 2)}, \
               {round(y, 2)})$ with value $\\approx {round(z, 2)}$"))

Линейный источник света [5 баллов]¶

Можем расширяться.

Теперь источником света будет не просто точка, а линия, поэтому формулу нужно преобразовать.

Лампа вдоль линии $t \in [-L; L]$ с координатами $(x_s, y_s, t, z_s)$ (где $x_s, y_s$ - фиксированное положение линии на плоскости, $t$ - координата вдоль линии, $z_s$ - высота линии над плоскостью) создаёт освещенность:

L(x, y) = \int_{-L}^L\frac{z_sdt}{((x-x_s)^2 + (y-y_s)^2 + t^2 + z_1^s)^\frac32}

# this was not linear at all ;-;
x = np.linspace(-1, 1, 200)
y = np.linspace(-1, 1, 200)
X, Y = np.meshgrid(x, y)

zs_line = 0.5       
L_len = 2.0         
N_line = 200        
t = np.linspace(-L_len, L_len, N_line)
dt = t[1] - t[0]

def linear_enlightenment(X, Y, t, zs):
  L_line = np.zeros_like(X)
  for ti in t:
      L_line += zs_line / (X**2 + (Y-ti)**2 + zs_line**2) ** 1.5 * dt
  
  return L_line

L_line = linear_enlightenment(X, Y, t, zs)

Нарисуем:

# 2D Heatmap
plt.figure(figsize=(6,5))
plt.imshow(L_line, extent=[-1,1,-1,1], origin='lower', cmap='inferno', norm=LogNorm())
plt.colorbar(label='L(x,y)')
plt.title('Линейный источник: 2D Heatmap')
plt.show()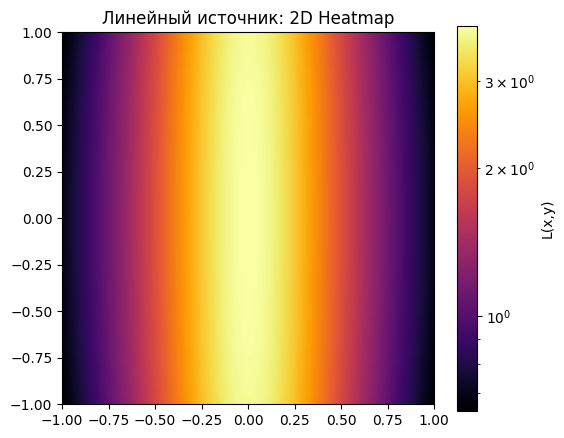

# 3D
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, L_line, cmap='inferno', linewidth=0, antialiased=True)
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('L(x,y)')
ax.set_title('Линейный источник: 3D Surface')
plt.show()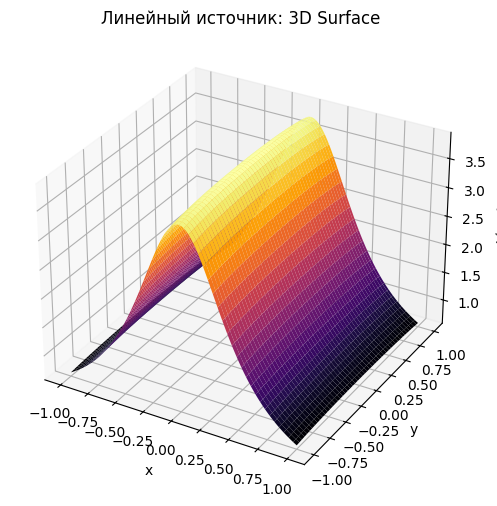

Задача 15.1 (0.5 балла)

Добавьте точечный источник и возьмите срез по $y = 0$ . Нарисуйте графики уровня освещенности по этому срезу, сравните, как отличается скорость падения у линейного и точечного источников. Сделайте выводы.

xs, ys, zs = 0, 0, 1

point = enlightenment(X, Y, xs, ys, zs)
L_total = L_line + point

x_slice = X[0, :]
L_slice = L_total[0, :]

plt.figure(figsize=(6,5))
plt.plot(x_slice, L_slice, label="Line + Point Lights")
plt.plot(x_slice, L_line[0, :], label="Linear Light")
plt.plot(x_slice, point[0, :], label="Point Light")
plt.xlabel('x')
plt.ylabel('L(x, y=0)')
plt.title('Slice at y=0 of the 3D field')
plt.grid(True)
plt.legend()
plt.show()

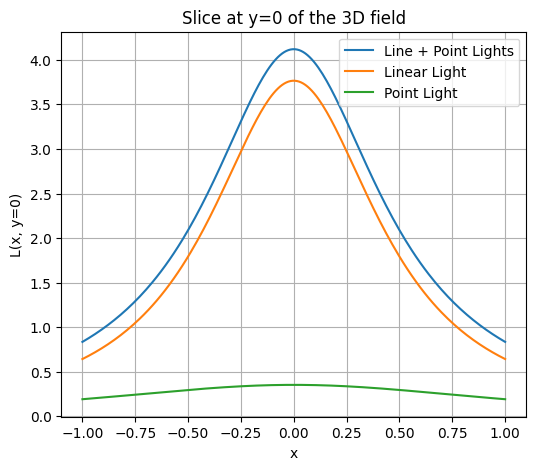
Luminosity of linear lights falls much faster along perpendicular slices since it is concentrated along its line. Lights that are next to each other intensify luminosities of each other greatly since their “light fields” intersect and combine well. As we stray further away from the line, light levels start dissipating much faster.

As for the pointed light, it dissipates much slower and more gradual since there is just a single light without anything else contributing to its intensity. Effectively, the difference is that plugging multiple lights in the same area would create a hotspot of light with some areas being overly bright and others much less bright than if we use a single source of light, which spreads luminosity more evenly over an area.

Задача 15.2 (4.5 балла)

В прошлом задании мы добавили точечный источник. В точке $S_p(x_s, y_s, z_s)$ . Получаем суммарную освещенность:

L_{\text{total}}(x, y) = L_{\text{lin}}(x, y) + L_{\text{pt}}(x, y)

Где $L_{\text{lin}}(x, y)$ результат функции linear_source, а с $L_{\text{pt}}$ мы знакомы из прошлого раздела.

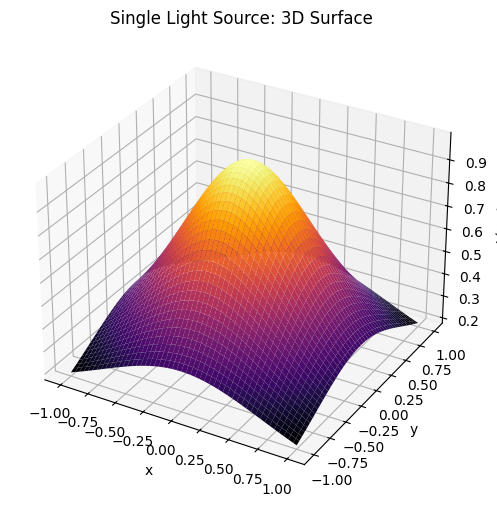
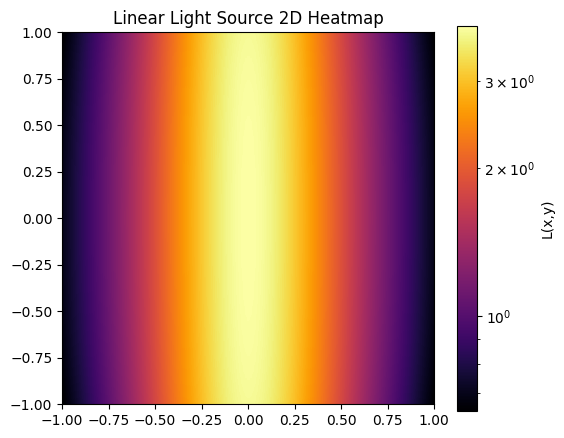
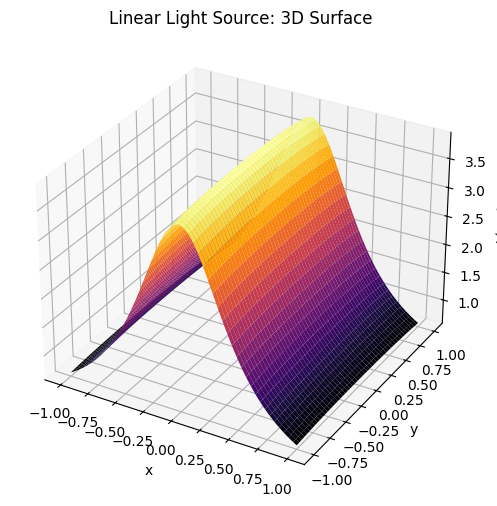
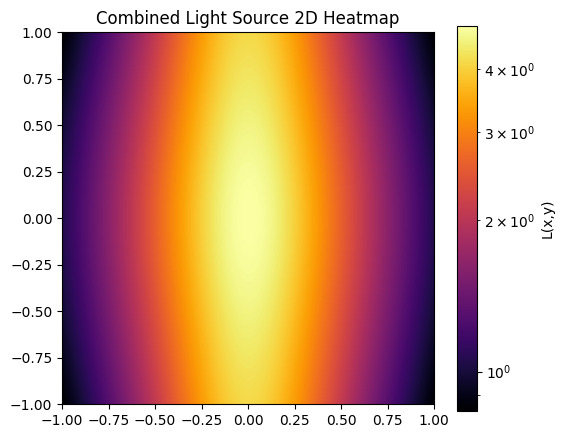
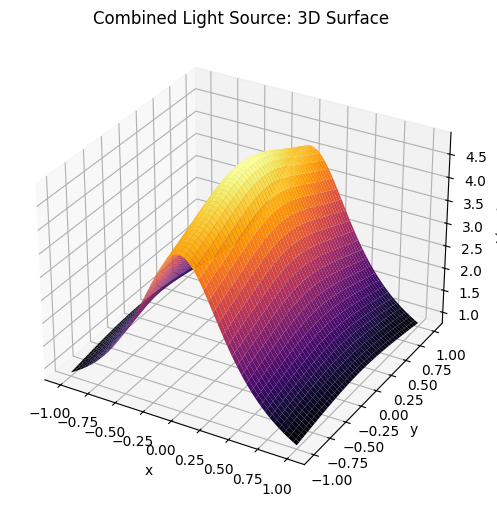
Постройте 2D heatmap и 3D surface для $L_{\text{lin}}$ , $L_{\text{pt}}$ , $L_{\text{total}}$ . Всего получится по 2 графика на каждый вариант.
Возьмите срез по y = 0 и постройте на одном графике кривые $L_{\text{lin}}(x, 0)$ , $L_{\text{pt}}(x, 0)$ , $L_{\text{total}}(x, 0)$ на оси $x \in [-1, 1]$ . Дополнительно постройте тот же срез в логарифмическом масштабе по оси Y, чтобы сравнить скорости падения.
Посчитайте полный интеграл освещенности $E = \iint\limits_D L_{\text{total}}(x, y)dxdy$ тремя способами (прямоугольники, трапеции и Монте-Карло), сравните полученные результаты с точным значением интеграла.
Исследуйте зависимость интеграла $E$ от размера сетки $N$ . Постройте график $E(N)$ и сделайте вывод о сходимости.

for graph, name in [(point, "Single Light Source"), (L_line, "Linear Light Source"), (L_total, "Combined Light Source")]:
    plt.figure(figsize=(6,5))
    plt.imshow(graph, extent=[-1,1,-1,1], origin='lower', cmap='inferno', norm=LogNorm())
    plt.colorbar(label='L(x,y)')
    plt.title(f'{name} 2D Heatmap')
    plt.show()

    fig = plt.figure(figsize=(8,6))
    ax = fig.add_subplot(111, projection='3d')
    ax.plot_surface(X, Y, graph, cmap='inferno', linewidth=0, antialiased=True)
    ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('L(x,y)')
    ax.set_title(f'{name}: 3D Surface')
    plt.show()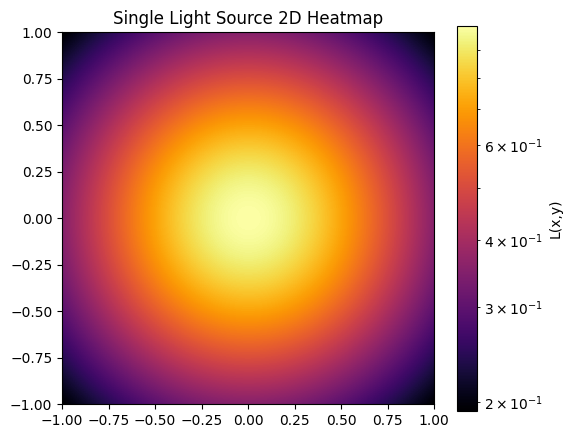

# The second point turned out to be identical to above,
# because it's an extension of the previous task,
# I'll just add a log scale version

plt.figure(figsize=(6,5))
plt.plot(x_slice, L_slice, label="Line + Point Lights")
plt.plot(x_slice, L_line[0, :], label="Linear Light")
plt.plot(x_slice, point[0, :], label="Single Light")
plt.yscale('log')
plt.xlabel('x')
plt.ylabel('L(x, y=0)')
plt.title('Slice at y=0 of the 3D field')
plt.grid(True)
plt.legend()
plt.show()

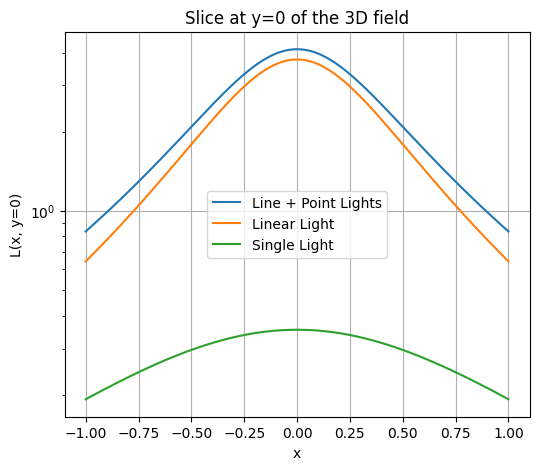
Introducing the log scale reinforces the notion that the graphs decrease with different asymptotics since the graph of the single light sources is squished.

# I was too lazy to write a proper function, so now I'm writing 
# spaghetti code everywhere, which I kinda regret, but let's 
# do the same thing for the kjghbillionth time

values = {"rect": [],
          "trap": [],
          "mc": []}

func = lambda x, y: linear_enlightenment(x, y, t, zs_line) + enlightenment(x, y, xs, ys, zs)
R = range(10, 101)

for N in R:
    x = np.linspace(-1,1,N)
    y = np.linspace(-1,1,N)
    X,Y = np.meshgrid(x,y)
    Z = func(X, Y)

    Z_trap = (Z[:-1,:-1] + Z[1:,:-1] + Z[:-1,1:] + Z[1:,1:])/4

    x_rand = np.random.uniform(-1,1,5000)
    y_rand = np.random.uniform(-1,1,5000)
    Z_rand = func(x_rand, y_rand)

    dx = x[1] - x[0]
    dy = y[1] - y[0]

    res_rect = np.sum(Z) * dx * dy
    res_trap = np.sum(Z_trap) * dx * dy
    res_mc = np.mean(Z_rand) * 4

    values["rect"].append(res_rect)
    values["trap"].append(res_trap)
    values["mc"].append(res_mc)

for type in ["rect", "trap", "mc"]:
    plt.plot(
      np.array(R),
      values[type],
      label=type
    )

result, _ = dblquad(func, -1, 1, lambda x: -1, lambda x: 1)
print(result)
print(abs(res_rect - result),
      abs(res_trap - result),
      abs(res_mc - result))

plt.title(f'Integral values relation')
plt.xlabel('$x$')
plt.ylabel('Function value')
plt.axhline(0, color='black', linewidth=0.5, ls='--')
plt.axvline(0, color='black', linewidth=0.5, ls='--')
plt.grid()
plt.ylim(10, 12)
plt.legend()

plt.show()

10.39583227731005
0.1321470883714202 0.000305528872868166 0.10267477906465494

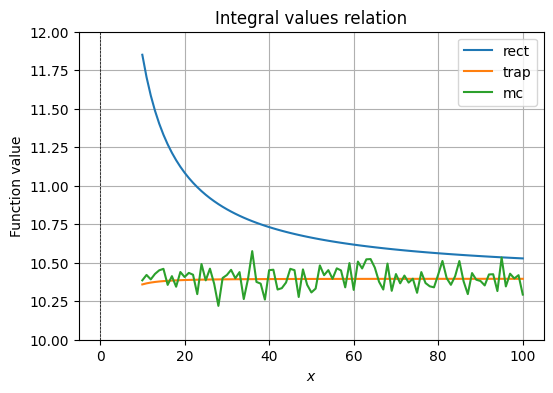
Conclusions are effectively the same as before! The rectangular approach very slowly allows estimating the integral, but at same values of $N$ , it is too imprecise. Trapezoids work really well as expected with functions of such type, whereas MC approximation is all over the place, but converges to the actual value with enough tries.

Тени от препятствий [3 балла]¶

Если на пути луча от источника до точки находится препятствие (например, стенка), свет не доходит до точки, и освещённость там считается равной нулю. Это простая модель тени, где мы не учитываем отражения, дифракцию и преломления.

Мы можем реализовать это через функцию shadow(x,y), которая проверяет, пересекает ли луч стенку:

def shadow(x, y, xs=xs, ys=ys, zs=zs):
    # Проверка пересечения с вертикальной стенкой x = 0.3
    if xs < 0.3 < x:
        return 0
    return zs / ((x-xs)**2 + (y-ys)**2 + zs**2)**(3/2)

# Параметры сетки
x = np.linspace(-1, 1, 200)
y = np.linspace(-1, 1, 200)
X, Y = np.meshgrid(x, y)

# Источник света
xs, ys, zs = 0.0, 0.0, 2.0

# Вычисление освещённости на сетке
Z_shadow = np.array([[shadow(xi, yi) for xi in x] for yi in y])

Визуализация тени показывает распределение освещённости с учётом препятствия.

# 2D
plt.figure(figsize=(6,5))
plt.imshow(Z_shadow, extent=[-1,1,-1,1], origin='lower', cmap='plasma')
plt.colorbar(label='Освещённость')
plt.title('Тени: 2D')
plt.xlabel('x'); plt.ylabel('y')
plt.show()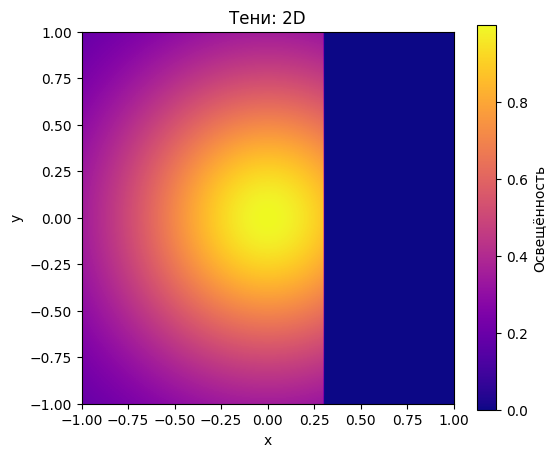

# 3D
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z_shadow, cmap='plasma')
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('L(x,y)')
ax.set_title('Тени: 3D')
plt.show()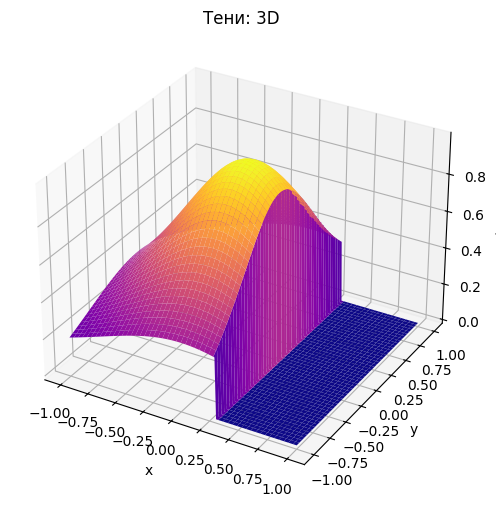

Не будем долго мудрить с примерами, а сразу перейдем к практике:

Задача 16 (3 балла)

Рассмотрим квадратную область $x, y \in [-1, 1]$ . Внутри области расположен круглый источник света радиуса $R$ , находящийся на стороне $z_s$ . Освещённость от этого источника в точке $(x, y)$ задаётся как интеграл по площади круга:

L_{\text{disk}}(x, y) = \iint\limits_{\text{disk}}\frac{z_sdx'dy'}{((x-x')^2 + (y-y')^2 + z_1^s)^\frac32}

где $(x', y')$ - точки внутри круга радиуса $R$ , центр круга находится в точке $(x_c, y_c)$ .

Реализуйте численное вычисление интеграла по кругу тремя методами и сравните результаты.
Постройте 2D heatmap и 3D surface для $L_{\text{disk}}$ .
Добавьте препятствие в виде вертикальной стенки $x = x_{\text{wall}}$ . В точках, где луч от любой точки круга пересекает стенку, освещённость = 0. Постройте новый 2D heatmap с учётом тени.
Вдоль линии $y = 0$ сделайте срез и покажите, как распределение освещённости меняется из-за тени и формы источника.

# круглый источник
x_c, y_c = 0.0, 0.0
R = 0.3
z_s = 0.5

x_wall = 0.2

values = {"rect": [],
          "trap": [],
          "mc": []}

def round_enlightenment(x, y, x_c, y_c, R, zs, N): 
    _x = np.linspace(x_c-R,x_c+R,N)
    _y = np.linspace(y_c-R,y_c+R,N)
    X,Y = np.meshgrid(_x,_y)

    mask = (X - x_c) ** 2 + (Y - y_c) ** 2 <= R ** 2
    Xg, Yg = X[mask].ravel(), Y[mask].ravel()

    dx = 2 * R / N
    dy = 2 * R / N

    L_circle = np.zeros_like(x)

    for xi, yi in zip(Xg, Yg):
        L_circle += zs / ((x - xi) ** 2 + (y - yi) ** 2 + zs ** 2) ** (3 / 2)
    
    return L_circle * dx * dy

_range = range(2, 30)
func = lambda x, y: round_enlightenment(x, y, x_c, y_c, R, zs, 100)
for N in _range:

    x = np.linspace(x_c-R,x_c+R,N)
    y = np.linspace(y_c-R,y_c+R,N)
    X,Y = np.meshgrid(x,y)

    Z = func(X, Y)

    Z_trap = (Z[:-1,:-1] + Z[1:,:-1] + Z[:-1,1:] + Z[1:,1:])/4

    x_rand = np.random.uniform(x_c-R, x_c+R,5000)
    y_rand = np.random.uniform(x_c-R, x_c+R,5000)
    Z_rand = func(x_rand, y_rand)

    dx = x[1] - x[0]
    dy = y[1] - y[0]

    res_rect = np.sum(Z) * dx * dy
    res_trap = np.sum(Z_trap) * dx * dy
    res_mc = np.mean(Z_rand) * (2 * R) ** 2

    values["rect"].append(res_rect)
    values["trap"].append(res_trap)
    values["mc"].append(res_mc)

print(values)

for type in ["rect", "trap", "mc"]:
    plt.plot(
      np.array(_range),
      values[type],
      label=type
    )

plt.title(f'Integral values relation')
plt.xlabel('$x$')
plt.ylabel('Function value')
plt.axhline(0, color='black', linewidth=0.5, ls='--')
plt.axvline(0, color='black', linewidth=0.5, ls='--')
plt.grid()
plt.legend()

plt.show()

{'rect': [0.7000889892749274, 0.4854101683609322, 0.4076027168338307, 0.3691551031458556, 0.3463799943171471, 0.3313501934842628, 0.32069942106888477, 0.31276131969969184, 0.3066184237782464, 0.30172450866432, 0.29773428098109705, 0.2944188580661963, 0.2916205653336564, 0.28922726332585585, 0.2871570277721256, 0.285348621279906, 0.28375535493000115, 0.28234101213717666, 0.28107706965589274, 0.2799407585817925, 0.27891368343940887, 0.2779808205930644, 0.27712977977606124, 0.27635025150122705, 0.2756335879780156, 0.2749724813703959, 0.27436071400676376, 0.27379296244768486], 'trap': [0.17502224731873184, 0.23831918112696315, 0.2496104767715575, 0.25354067679348774, 0.25535711989718435, 0.25634318228832426, 0.2569375348805289, 0.25732320901643313, 0.2575875884129846, 0.2577766788732967, 0.2579165745207757, 0.25802297101558086, 0.2581057691590127, 0.25817146487131437, 0.25822446348100103, 0.2582678380713488, 0.2583037852654949, 0.2583339089419215, 0.2583594023077742, 0.2583811679124209, 0.25839989864995616, 0.2584161335977531, 0.25843029724436367, 0.25844272752303604, 0.2584536961583213, 0.2584634236436016, 0.2584720904097631, 0.25847984525307965], 'mc': [0.25875310425695003, 0.25864604776265215, 0.25757396771030183, 0.2588234756085421, 0.258365584221401, 0.2582036401756298, 0.25846495931311225, 0.2589616445997444, 0.25771179719051596, 0.2595377516715922, 0.258935813449701, 0.2586824367875529, 0.2586989089336001, 0.25886568809459054, 0.2590608935006158, 0.2579085807968907, 0.2590670937982294, 0.25887897350133315, 0.2584459458574917, 0.25825000888972877, 0.2580519204126356, 0.2586345432258985, 0.2584552857467275, 0.2587818939166918, 0.2587755608448108, 0.25906920098198594, 0.2583196241486038, 0.2589644336834504]}

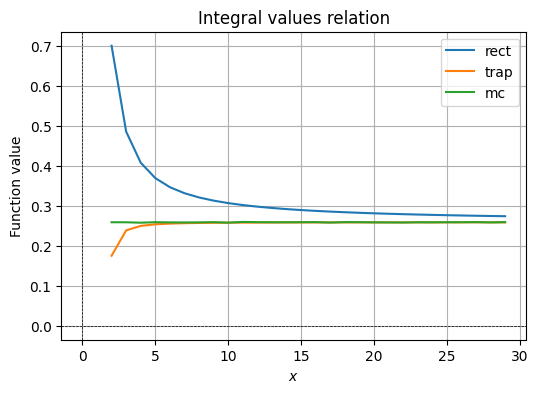
plt.figure(figsize=(6,5))
plt.imshow(func(X, Y), extent=[-1,1,-1,1], origin='lower', cmap='inferno', norm=LogNorm())
plt.colorbar(label='L(x,y)')
plt.title(f'Disk Light Source 2D Heatmap')
plt.show()

fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, func(X, Y), cmap='inferno', linewidth=0, antialiased=True)
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('L(x,y)')
ax.set_title(f'Disk Light Source  3D Surface')
plt.show()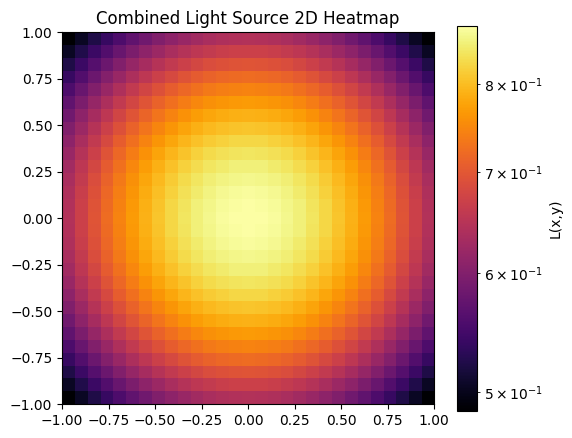

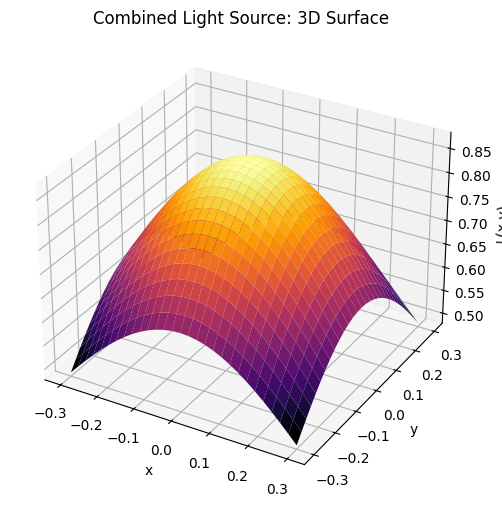
def shadowed(func, X, Y, x_wall):
    L = func(X, Y).copy()
    L[X > x_wall] = 0
    return L

target_func = shadowed(func, X, Y, x_wall)

plt.figure(figsize=(6,5))
plt.imshow(target_func, extent=[X.min(), X.max(), Y.min(), Y.max()], origin='lower', cmap='inferno', norm=LogNorm())
plt.colorbar(label='L(x,y)')
plt.title(f'Shadowed Disk 2D Heatmap')
plt.show()

fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, target_func, cmap='inferno', linewidth=0, antialiased=True)
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('L(x,y)')
ax.set_title(f'Shadowed Disk 3D Surface')
plt.show()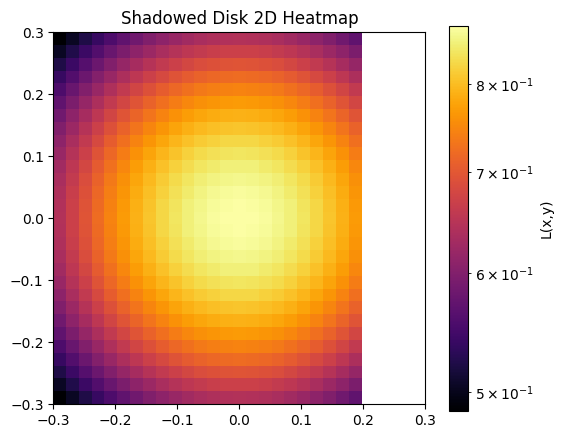

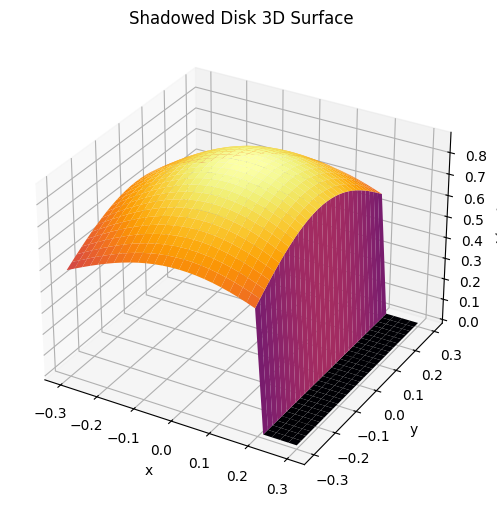
plt.figure(figsize=(6,5))
plt.plot(X[0, :], target_func[0, :], label="Shadowed Disk at y=0")
plt.xlabel('x')
plt.ylabel('L(x, y=0)')
plt.title('Slice at y=0 of the 3D field')
plt.grid(True)
plt.legend()
plt.show()

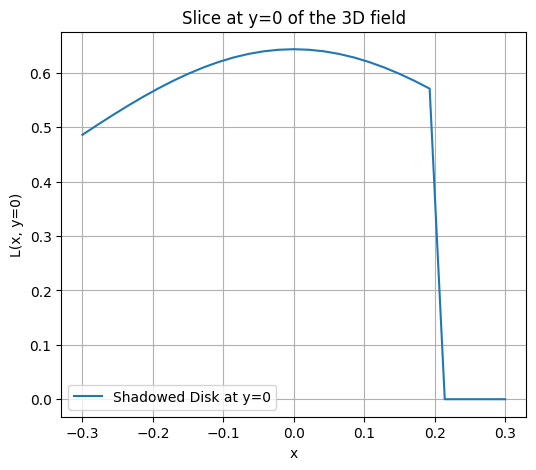
Conclusions:

First of all, trying to make the disk light source work was quite a nightmare, but other than that, the task was pretty straightforward since it expands on what we have been doing before. Effectively, we cut off a part of the luminosity graph, which is represented by a wall if we were to draw alternatives to the real world.

It is fair to say that the line on the slice graph is not straight, but this is due to large granularity, because calculating double integrals twice in iteration has ridiculous asymptotics, so I decided not to wait it out or optimize anything further, and just let it be. It should be straight.

Tbh, not sure what else to say, we have just added a wall, the drawn conclusion should be trivial.

Материал поверхности и отражения [8 баллов]¶

Помните, выше было написано про закон Ламберта? Именно он нам сейчас понадобится.

При диффузном отражении отражённая освещённость пропорциональна падающей:

L_{\text{diff}}(x, y) = \rho \cdot L_{\text{inc}}(x, y)

где $\rho \in (0, 1)$ - коэффициент отражения, а $L_{\text{inc}}$ - падающая освещенность.

При этом суммарная освещенность на области $D$ всё так же будет вычисляться как

E = \iint\limits_D L_{\text{diff}}(x, y)dxdy

Теперь посмотрим как это будет выглядеть:

# Сетка
x = np.linspace(-1, 1, 100)
y = np.linspace(-1, 1, 100)
X, Y = np.meshgrid(x, y)

z_s = 0.5
L_inc = z_s / ((X**2 + Y**2 + z_s**2)**1.5)
L_max = np.max(L_inc)

# 2D
out2d = Output()

def plot_2d(rho=0.5):
    with out2d:
        out2d.clear_output(wait=True)
        L_diff = rho * L_inc

        dx = x[1] - x[0]
        dy = y[1] - y[0]
        E_total = np.sum(L_diff) * dx * dy

        plt.figure(figsize=(6,5))
        plt.imshow(L_diff, extent=[-1,1,-1,1], origin='lower', cmap='coolwarm', vmin=0, vmax=L_max)
        plt.colorbar(label='L_diff')
        plt.title(f'Фиксированный материал, ρ={rho} - 2D heatmap\nСуммарная освещённость E ≈ {E_total:.4f}')
        plt.show()

interact(plot_2d, rho=(0.0, 1.0, 0.05))
display(out2d)

# 3D
out3d = Output()

def plot_3d_fixed(rho=0.5):
    with out3d:
        out3d.clear_output(wait=True)
        L_diff = rho * L_inc
        dx = x[1] - x[0]
        dy = y[1] - y[0]
        E_total = np.sum(L_diff) * dx * dy

        fig = plt.figure(figsize=(8,6))
        ax = fig.add_subplot(111, projection='3d')
        surf = ax.plot_surface(
            X, Y, L_diff,
            cmap='coolwarm',
            linewidth=0, antialiased=True
        )
        surf.set_clim(0, L_max)
        fig.colorbar(surf, ax=ax, label='L_diff')

        ax.set_xlabel('x')
        ax.set_ylabel('y')
        ax.set_zlabel('L_diff')
        ax.set_zlim(0, L_max)
        ax.set_title(f'Фиксированный материал, ρ={rho} - 3D surface\nСуммарная освещённость E ≈ {E_total:.4f}')
        plt.show()

interact(plot_3d_fixed, rho=(0.0, 1.0, 0.05))
display(out3d)

Задача 17.1 (0.5 балла)

У нас есть интерактивный ползунок для коэффициента отображения $\rho$ . Понаблюдайте за тем, как изменяются графики и объясните наблюдаемое поведение при уменьшении $\rho$ .

Свяжите визуальные эффекты с физическим смыслом уменьшения коэффициента отражения (статья на вики).

As $\rho$ decreases, less luminosity gets redirected back at the viewer overall, which can be clearly observed from the graphs, given that we only plot the refracted light from a source and not the total luminosity. This is connected with real-world fact that the smaller the reflection coefficient is, less light would it reflect. At $\rho=1$ we could observe the shape of the light source itself, whereas if the material does not reflect light $\rho=0$ , then there would be nothing.

Теперь рассмотрим градиент.

Если материал неоднородный, то $\rho$ зависит от координат и в этом случае модель градиента задается как

\rho_\text{grad}(x,y) = \max\Big(0, 1 - \frac{(x-c_x)^2 + (y-c_y)^2}{R^2}\Big)^\text{power}

где $(c_x, c_y)$ — координаты центра “пика” освещённости, $R$ — радиус, который определяет область влияния пика, $\text{power}$ — регулирует крутизну пика (чем больше, тем резче подъем).

Логично, свет отражается сильнее в области с большим $\rho$ а пики отражённой освещённости смещаются по области.

Поработаем с конкретным примером:

\rho(x, y) = \left(\frac{x+1}{2}\right)^2\left(\frac{y+1}{2}\right)^2

# 2D
out_grad2d = Output()

rho_grad_shifted = ((X+1)/2)**2 * ((Y+1)/2)**2
L_diff_grad_shifted = rho_grad_shifted * L_inc

def plot_grad_2d():
    with out_grad2d:
        out_grad2d.clear_output(wait=True)
        data = L_diff_grad_shifted

        dx = x[1] - x[0]
        dy = y[1] - y[0]
        E_total = np.sum(data) * dx * dy

        plt.figure(figsize=(6,5))
        plt.imshow(data, extent=[-1,1,-1,1], origin='lower', cmap='coolwarm')
        plt.colorbar(label='L_diff')
        plt.title(f'Градиентный материал - 2D\nСуммарная освещённость E ≈ {E_total:.4f}')
        plt.show()

plot_grad_2d()
display(out_grad2d)

# 3D
out_grad3d = Output()

def plot_grad_3d_shifted_fixed():
    with out_grad3d:
        out_grad3d.clear_output(wait=True)
        data = L_diff_grad_shifted

        dx = x[1] - x[0]
        dy = y[1] - y[0]
        E_total = np.sum(data) * dx * dy

        fig = plt.figure(figsize=(8,6))
        ax = fig.add_subplot(111, projection='3d')
        ax.plot_surface(X, Y, data, cmap='coolwarm', linewidth=0, antialiased=True)

        ax.set_xlabel('x')
        ax.set_ylabel('y')
        ax.set_zlabel('L_diff')
        ax.set_title(f'Градиентный материал - 3D\nСуммарная освещённость E ≈ {E_total:.4f}')

        plt.show()

plot_grad_3d_shifted_fixed()
display(out_grad3d)

Задача 17.2 (0.5 балла)

Почему итоговое значение суммарной освещенности так сильно отличается у фиксированного материала и градиентного?

A single, fixed material, would reflect an amount of light stably proportional to the amount of light it catches. Regardless of the position of the light source given an infinitely large wad of material, the total luminosity would be the same regardless of the source’s position.

Luminosity of a gradient material, on the other hand, largely depends on how reflective the part of the surface is that catches most of the light. This may lead to drastic differences in reflected luminosity given the same other conditions.

Задача 17.3 (2.5 балла)

Возьмите срез по линии $y = 0.5$ и постройте на одном графике кривые отражённой освещённости для фиксированного материала $L_\text{fixed}(x, y_\text{line})$ ( $\rho$ возьмите равным 0.5) и градиентного материала $L_\text{grad}(x, y_\text{line})$ на оси $x \in [-1, 1]$

Исследуйте влияние положения линии среза $y_\text{line}$ на форму кривых градиентного материала. Попробуйте взять несколько значений $y_\text{line}$ и сравните результаты.

Проанализируйте различия между фиксированным и градиентным материалом. Объясните, почему кривые градиентного материала изменяются сильнее при изменении линии среза и как это отражается на логарифмическом графике.

rho_fixed = 0.5

L_first = rho_fixed * L_inc
L_second = L_diff_grad_shifted

for cy in [-1, -0.75, -0.5, -0.25, 0, 0.25, 0.5, 0.75, 1]:

    index = np.argmin(np.abs(Y[:, 0] - cy))

    plt.figure(figsize=(8,5))
    plt.plot(X[0, :], L_first[index, :], label="fixed")
    plt.plot(X[0, :], L_second[index, :], label="gradient")
    plt.xlabel('x')
    plt.ylabel('L_diff')
    plt.title(f'Slice of 3D surface at y={cy}')
    plt.grid(True)
    plt.legend()
    plt.ylim(0, 2)
    plt.show()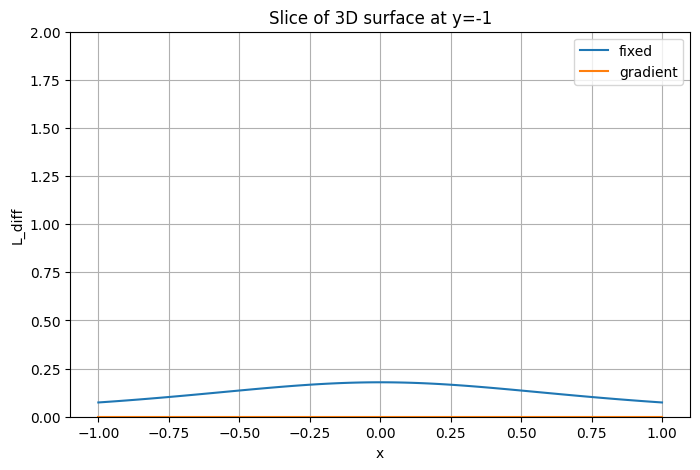


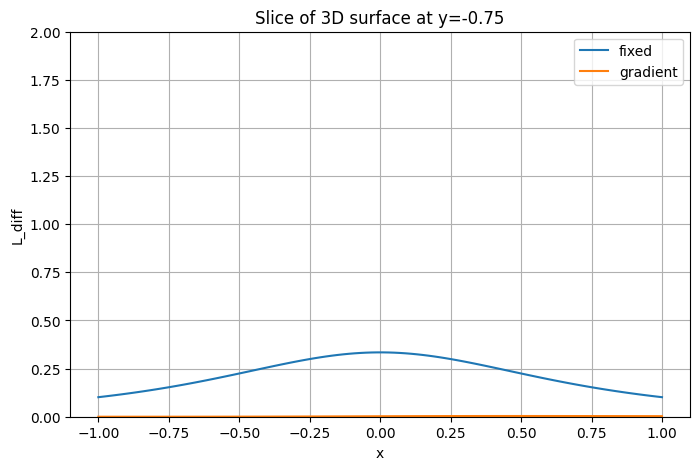
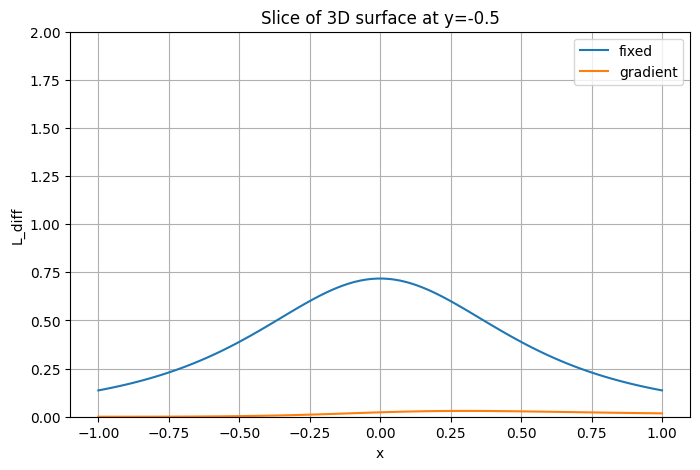
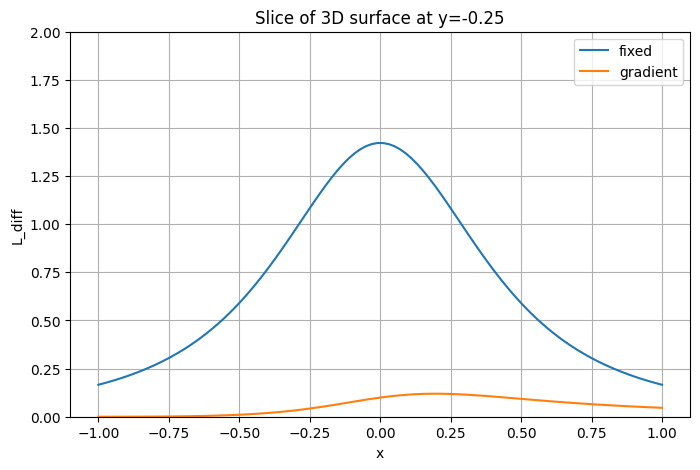
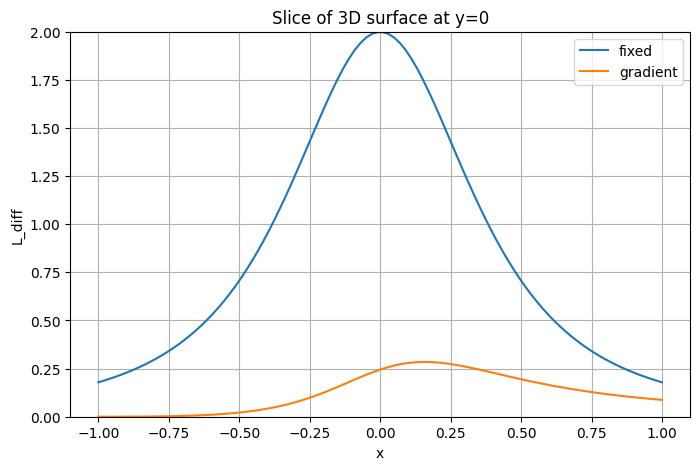
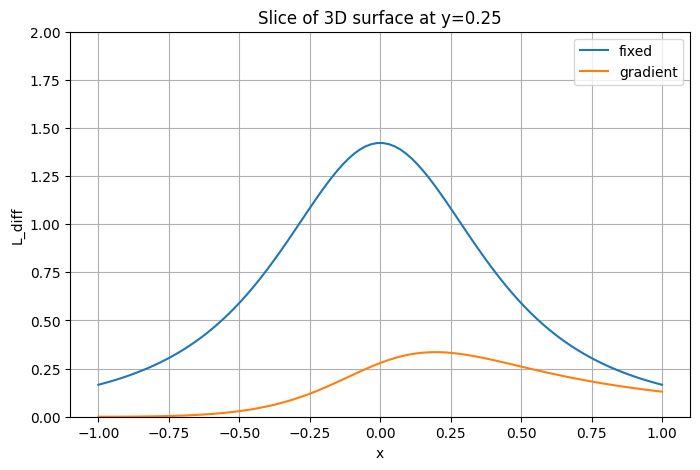
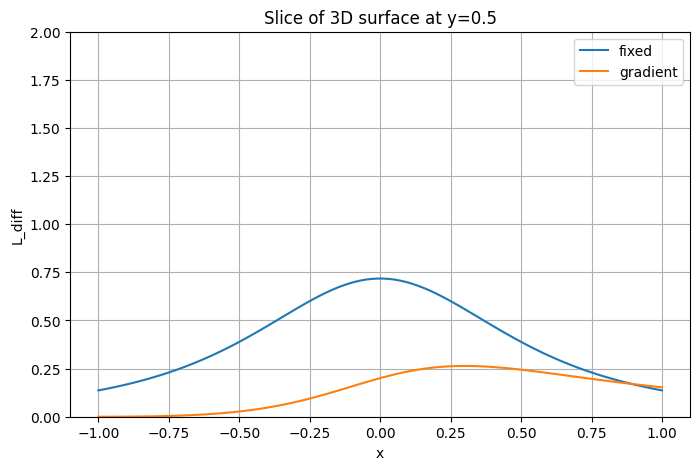
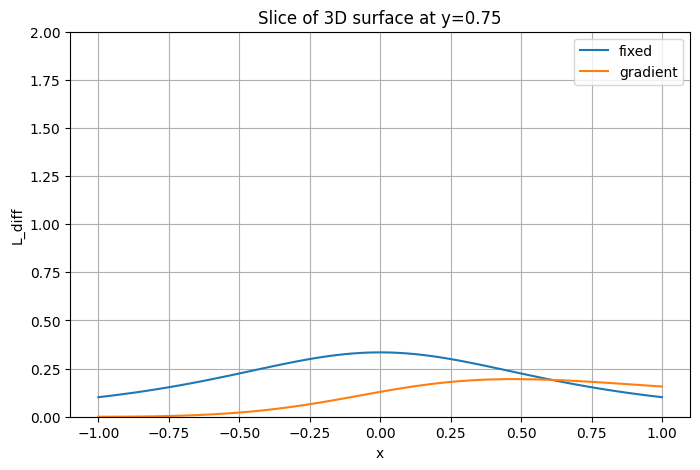
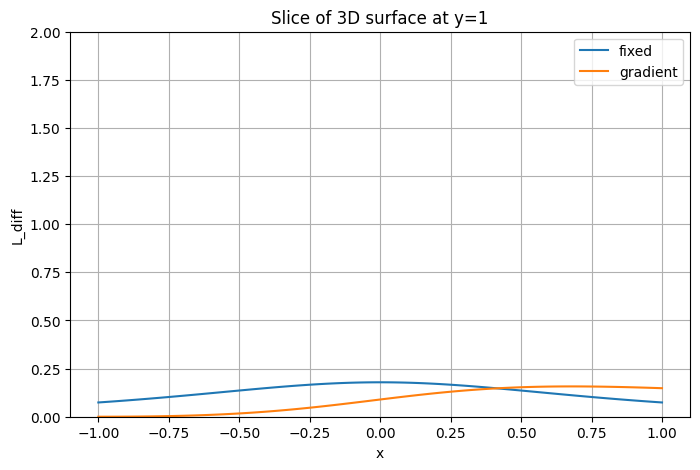
for cy in [-1, -0.75, -0.5, -0.25, 0, 0.25, 0.5, 0.75, 1]:

    index = np.argmin(np.abs(Y[:, 0] - cy))

    plt.figure(figsize=(8,5))
    plt.plot(X[0, :], L_first[index, :], label="fixed")
    plt.plot(X[0, :], L_second[index, :], label="gradient")
    plt.xlabel('x')
    plt.ylabel('L_diff')
    plt.title(f'Slice of 3D surface at y={cy} (log)')
    plt.grid(True)
    plt.legend()
    plt.yscale("log")
    plt.show()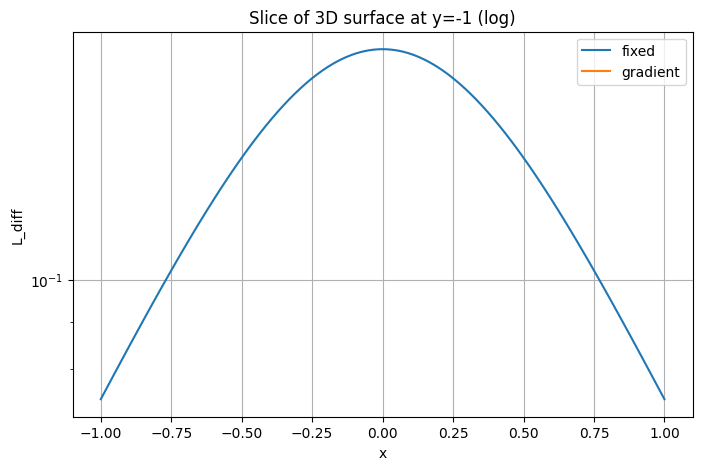

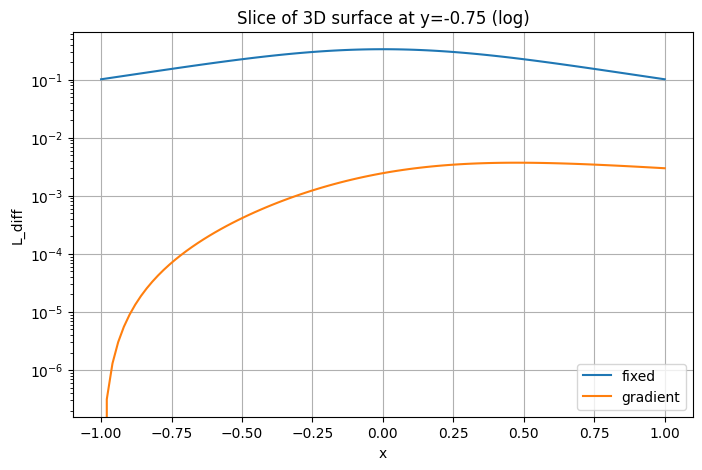
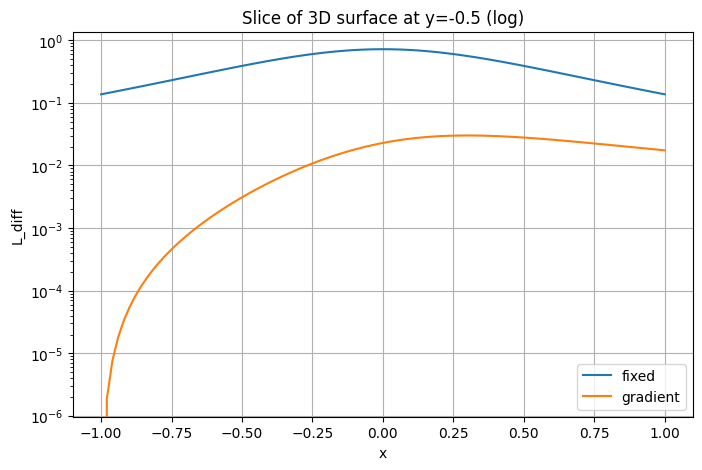
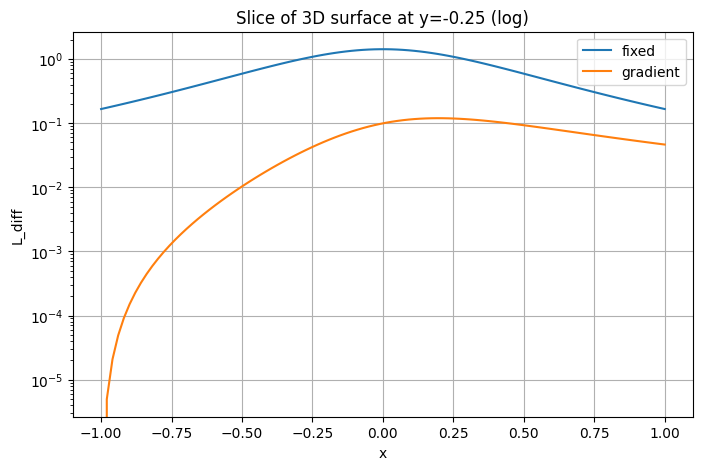
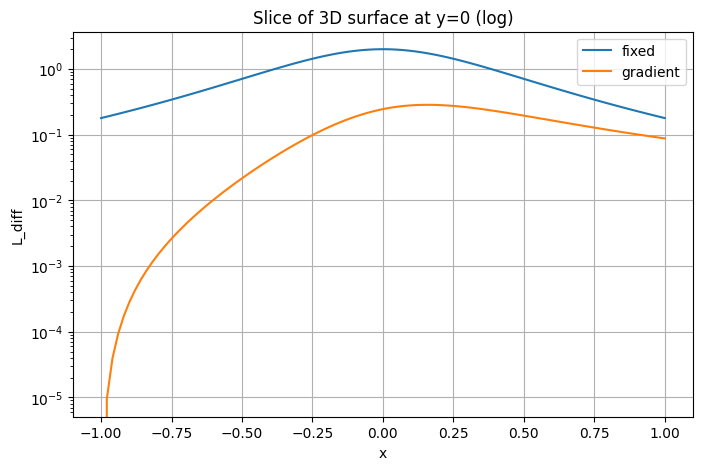
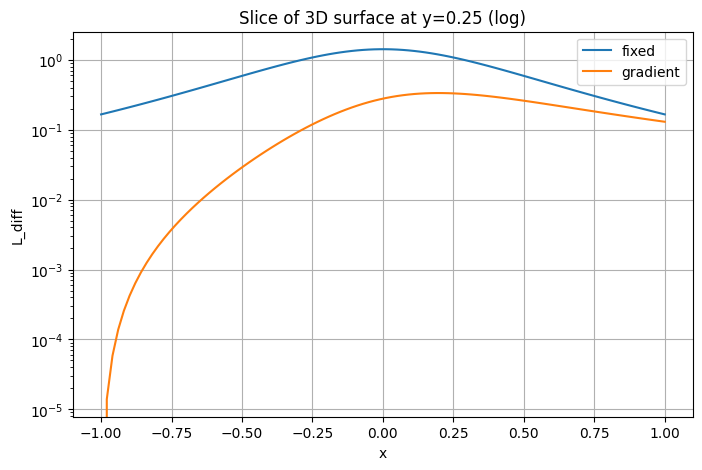
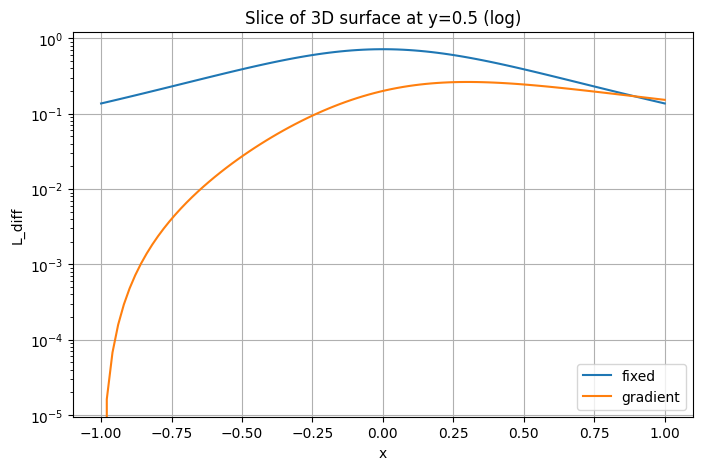
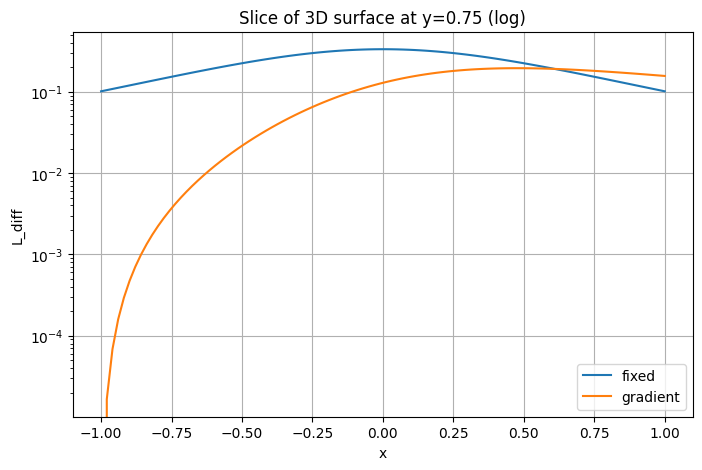
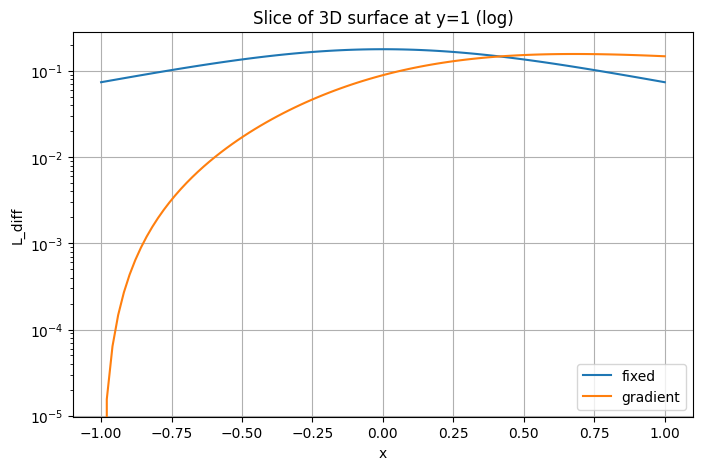
The main thing that can be observed is that fixed material slices are plotted symmetrically and change very smoothly as we go through different values of $y$ . Gradient, on the other hand, is a much more interesting creature. As we stray towards the vertex of the gradient, we approach a peak where the reflection is maximal and for certain $y$ can even surpass the fixed material’s.

Additionally, the speed with which reflection changes for the gradient is large logarithmically, because going from left to right in case, we clearly observe how much higher the points on the right of the plot are.

As we approach the gradient’s peak with the highest values, the change would be even more noticeable as we go from pathetically small values to the highest of the highest. Such cannot be observed for the fixed material since its changes are quite stable everywhere.

Задача 17.4 (4 балла)

В качестве последнего задания этой части вам предстоит реализовать интерактивную визуализацию отражённой освещённости для градиентного материала.

Цель — понаблюдать, как изменяется форма и величина отражённой освещённости при смещении центра градиента и изменении крутизны “пика” освещённости.

Чуть подробнее о том, что нужно сделать:

Используйте формулу для $\rho(x, y)$ в общем виде, сделайте интерактивные ползунки для $c_x, c_y, \text{power}$ , чтобы наблюдать, как смещается максимум освещённости и изменяется её распределение.
Используя построенное распределение отражённой освещённости вычислите суммарную освещенность на области $D$ . Реализуйте три способа численного вычисления интеграла: метод прямоугольников, метод трапеций и метод Монте-Карло.
Сравните результаты и сделайте выводы о влиянии положения и крутизны градиента на суммарную освещённость.

# Сетка
x = np.linspace(-1, 1, 100)
y = np.linspace(-1, 1, 100)
X, Y = np.meshgrid(x, y)

R = 2 ** 0.5 # радиус

values = {"rect": [],
          "trap": [],
          "mc": []}

func = lambda x, y: linear_enlightenment(x, y, t, zs_line) + enlightenment(x, y, xs, ys, zs)
R = range(10, 101)

for N in R:
    x = np.linspace(-1,1,N)
    y = np.linspace(-1,1,N)
    X,Y = np.meshgrid(x,y)
    Z = func(X, Y)

    Z_trap = (Z[:-1,:-1] + Z[1:,:-1] + Z[:-1,1:] + Z[1:,1:])/4

    x_rand = np.random.uniform(-1,1,5000)
    y_rand = np.random.uniform(-1,1,5000)
    Z_rand = func(x_rand, y_rand)

    dx = x[1] - x[0]
    dy = y[1] - y[0]

    res_rect = np.sum(Z) * dx * dy
    res_trap = np.sum(Z_trap) * dx * dy
    res_mc = np.mean(Z_rand) * 4

    values["rect"].append(res_rect)
    values["trap"].append(res_trap)
    values["mc"].append(res_mc)

for type in ["rect", "trap", "mc"]:
    plt.plot(
      np.array(R),
      values[type],
      label=type
    )

result, _ = dblquad(func, -1, 1, lambda x: -1, lambda x: 1)
print(result)
print(abs(res_rect - result),
      abs(res_trap - result),
      abs(res_mc - result))

plt.title(f'Integral values relation')
plt.xlabel('$x$')
plt.ylabel('Function value')
plt.axhline(0, color='black', linewidth=0.5, ls='--')
plt.axvline(0, color='black', linewidth=0.5, ls='--')
plt.grid()
plt.ylim(10, 12)
plt.legend()

plt.show()

Напишите выводы сюда ᕙ(`▿´)ᕗ

Задача 17.5 (0.5 балла)

Здесь можно оставить мем или ответить на сложный теоретический вопрос:

Зачем людям нужны чайники?

Часть 4. Scale-Invariant Feature Transform¶

В этой части у вас могут (но не должны!) возникнуть проблемы с работоспособностью кода из-за разных способов вычисления дискретной производной. Для первой производной автор использовал формулу $\frac{f(x+1) - f(x - 1)}{2}$ , а для второй $f(x+1) - 2f(x) + f(x-1)$

Отбор изначальных кандидатов на признаки¶

SIFT (Scale-Invariant Feature Transform) - метод выделения устойчивых признаков, не зависящих от масштаба. Идея такая: строим гауссово масштабное пространство - одно и то же изображение в черно белом формате, размазанное Гауссом с разными $\sigma$ . Для того, чтобы не опираться на масштаб, нужно сравнивать между собой размытия с разной резкостью (действительно, если уменьшить фото в 2 раза все признаки остануться теми же, и так же будут обнаружены - просто при сравнении слоев с вдвое меньшим размытием). Однако, сравнивать сами размытия между собой неудобно, поэтому авторы метода предлагают сравнивать разность соседних размытий (Difference of Gaussians, DoG) подчёркивает структуры “своего” характерного размера. Тогда кандидаты в ключевые точки выбираем как локальные экстремумы DoG в трёхмерной окрестности $(x,y,\sigma)$ : точка должна быть больше (или меньше) всех соседей в своём слое и в двух соседних слоях по масштабу. Такое правило сразу даёт и координату, и оценку масштаба признака.

При таком подходе возникает проблема - для больших $\sigma$ соседние пиксели практически не будут отличаться по значению, и выделение признаков будет очень неустойчивым. Это можно исправить, если рассматривать “октавы” - различные масштабы картинок, которые будут размываться одними и теми же значениями $\sigma$ . Например, размытие картинки $2n\times 2n$ с $\sigma = 2\sigma_0$ будет аналогично размытию картинки $n\times n$ с $\sigma = \sigma_0$ , но с меньшем качеством во втором случае.

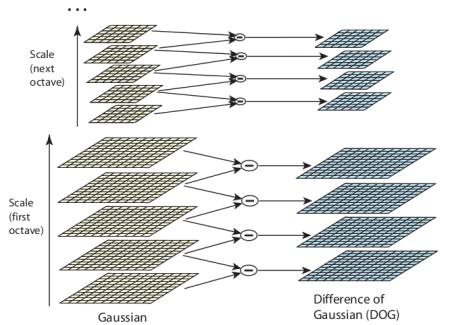
Понятно, что уменьшать можно не только в 2 раза, назовем этот параметр scale. В таком случае, для каждой октавы $\sigma_i = \sigma_0 \operatorname{scale}^{\frac{i}{S}}, i \in [0, S+2]$ , где $S$ - количество слоёв для поиска экстремумов.

Задача 18.1 (1 балл)

Объясните, почему нам нужны $S+3$ размытия.

Answer: Each adjacent pair of Gaussian blur layers from a set spawns its own DOG layer. Therefore, the total number of DOG layers would be one less than the number of Gaussian blur layers. We got $S+3\rightarrow S+2$ , let’s see further. The minimum number of layers $S$ is 1, so we should prove that $S+2=3$ is the minimum required number of such layers.

However, in order to correctly find extremums, we need a layer above and below each layer we would be comparing (minimum 3 in total). Therefore, the minimum number of possible layers is $S+2$ , which requires one more Gaussian blur layer: $S+3$ .

Понятно, что увеличивать число октав выше какого-то значения нельзя - как минимум, в какой-то момент картинка сожмется в 1 пиксель.

Задача 18.2 (1 балл)

Предложите способ, которым можно оценивать число октав по размерам фотографии, и реализуйте его.

def get_octaves(height: int, width: int, *args, **kwargs) -> int:
    # take the smallest side to consider
    # taking the logarithm of the smallest side would give us
    # the possible number of times a side could be split in two
    # thus, take that number of splits, as well as one more possible octave
    return math.floor(math.log2(min(height, width))) + 1

Задача 19.1 (1 балл)

Пришло время реализовать вычисление ключевых точек. Напишите своё Гауссово размытие используя функции fft, которые вы писали в прошлых частях. Если параметр pad == 'mirror', то вы должны дополнить изображение отражениями, чтобы по краям не было черных полос. Так же, докажите, что композиция Гауссовых размытий с параметрами $\sigma_1$ и $\sigma_2$ - Гауссово размытие, и найдите значение $\sigma_3(\sigma_1, \sigma_2)$

Доказательство:

def gaussian_blur(img: np.ndarray, sigma: float, pad: str = '') -> np.ndarray:
    H, W = img.shape
    
    if pad == 'mirror':
        img_padded = np.pad(img, ((H, H), (W, W)), mode='reflect')
    else:
        img_padded = img
    
    H_p, W_p = img_padded.shape
    
    y = np.fft.fftfreq(H_p)[:, None]
    x = np.fft.fftfreq(W_p)[None, :]
    gaussian_kernel = np.exp(-2 * (np.pi**2) * sigma**2 * (x**2 + y**2))
    
    img_fft = FFT(img_padded)
    img_blurred = IFFT(img_fft * gaussian_kernel).real
    
    if pad == 'mirror':
        img_blurred = img_blurred[H:H+H, W:W+W]
    
    return img_blurred

Как правило, фотографии снятые на камеру не являютсся абсолютно четкими - из-за тряски, разного расстояния до объектов, несовершенства линз, волновой природы, света и т.д. многие части получаются слегка размытыми.

Задача 19.2

Предлагается это учесть путем “доблюра” фото, приняв, что оно изначально немного размыто Гауссом с $\sigma = \operatorname{sigma\_ in}$ , до размытия $\sigma_0$ .

Зная результат из Задачи 19.1 можно немного ускорить вычисление всех необходимых масштабов за счет уменьшения ядра свёртки. Настоятельно прошу вас писать алгоритм именно на этом принципе, так как ускорение с 4 минут до 3 уже является ощутимымм.

# params example
# params = {
#     'octaves': 12,
#     'S': 3,
#     'sigma0': 1.6,
#     'sigma_in': 0.5,
#     'pad': 'mirror',
# }

def build_gaussian_pyramid(img_gray: np.ndarray, params: dict) -> list[list[np.ndarray]]:
    # YOUR CODE HERE
    raise NotImplementedError()

Теперь, с помощью build_gaussian_pyramid реализуйте вычисление DoG

def build_DoG_pyramid(gauss_pyr: list[list[np.ndarray]]) -> list[list[np.ndarray]]:
    # YOUR CODE HERE
    raise NotImplementedError()

Теперь, у нас есть всё необходимое для поиска изначальных кандидатов на роль признаков инвариантных к масштабу. Для того, чтобы в дальшенйшем было проще работать с точками, используйте класс Keypoint. Поле orientation нам понадобится позже. Координаты $x$ и $y$ берутся на том же масштабе, что и сама точка, не надо вычислять их для оригинального масштаба (пока). Так же, чтобы не выбирать точки слабо отличающиеся от 26 соседей (8 на той же DoG, и ещё 18 на соседних), есть параметр threshold.

@dataclass
class Keypoint:
    octave_index: int
    s_index: int
    y: float
    x: float
    sigma: float
    orientation: Optional[float] = None

def find_extrema(
    dog_pyr: list[list[np.ndarray]],
    S: int,
    sigma0: float,
    threshold: float = 0.03
) -> list[Keypoint]:
    kps = []
    # YOUR CODE HERE
    raise NotImplementedError()
    return kps

Уточнение положения¶

Так как почти все слои, на которых вычислялись конкретные положения точек имеют меньший масштаб, чем оригинальное фото, для того, чтобы признаки можно было хорошо сопоставить, необходимо уточнить их положение (например, уже на 3 октаве координаты могут быть сдвинуты уже на 8 оригинальных пикселей, при изменении масштаба в 2 раза, а октав обычно намного больше).

Но мы можем опереться на то, что то, что мы нашли находится близко к истинному максимуму. Поэтому, для уточнения мы прибегнем к методу Ньютона. Вкратце о нем: если координата находится близко к экстремуму, то можно приблизить функцию квадратичной, и ожидать, что экстремум приближения будет намного ближе к истинному, чем изначальная точка.

Так как функция $D(x, y, s)$ зависит от 3 параметров, её разложение (если оно существует в таком виде, но на практике предпологаем, что это так) будет выглядеть следующим образом:

D(p) \approx D(p_0) + (\nabla D(p_0))^T \Delta p + \frac12 \Delta p^T \nabla^2 D(p_0) \Delta p, \quad p = \begin{pmatrix} x\\ y\\ z\\ \end{pmatrix}

У экстремума $\nabla D = 0$ . Из этого следует, что сдвиг до координаты обновленного экстремума $\Delta \hat{p} = - (\nabla^2 D(p_0))^{-1}$ и $D(\Delta \hat{p}) = D(p_0) + \frac12 (\nabla D(p_0))^T \Delta \hat{p}$ .

Так как у нас не непрерывный, а дискретный случай, придется немного отойти от оригинального метода Ньютона. В случае, если изменение по какой либо из координат становиться больше 0.5 - то есть, предполагаемый экстремум находится ближе к соседней координате, то мы повторяем вычисления для неё. В случае, если сдвиг не вриводит в соседнюю координату, надо смотреть на приближение истинного значения $D(\Delta \hat{p}) \leq 1$ - если это значение мало, то можно предположить, что это несущественный признак (так как мы смотрим на максимум, а если максимум находится около нуля - наверное, это шум). В случае, если мы за определенное количество итераций не сошлись к какой то точке, то мы отбрасываем эту координату. В рамках данной работы используйте $\operatorname{threshhold}=0.03, \operatorname{max\_ iter}=5$ .

Так же, обратите внимание, что матрица $\nabla^2 D(p_0)$ может быть близка к вырожденной и тогда численно могут получаться странные значения. Как правильно поступать в таких ситуациях рассказывают на курсе по основам матричных вычислений, а пока что для нахождения $- (\nabla^2 D(p_0))^{-1}$ используйте np.linalg.solve, и при возникновении ошибок - отбрасывайте точку.

def localize_keypoint(
    dog_pyr: list[list[np.ndarray]],
    kp: Keypoint,
    S: int,
    sigma0: float,
    threshhold: float = 0.03,
    max_iter: int = 5
) -> Optional[Keypoint]:
    # YOUR CODE HERE
    raise NotImplementedError()

Задача 20 (8 баллов)

Для того, чтобы проверить себя, выберите понравившееся вам фото, и нарисуйте на нем точки до и после локализации - они должны быть похожи. Проследите, чтобы разные точки не перекрывали друг друга, и отличались по цвету. Картинка должна быть черно-белой.

# YOUR CODE HERE

Отсеивание признаков с границ объектов¶

Задача 21.1 (1 балл)

Нам необходимо убрать признаки, лежащие на прямых границах объектов. Объясните, почему?

Ваш ответ:

Для этого так же будем предполагать, что функция $D(x, y)$ (уже без $s$ , так как мы не уточняем положение, а фильтруем точки для конкретных слоев!) хорошо аппроксимируется квадратичной функцией.

Задача 21.2 (1 балл)

С помощью $\nabla^2 D(x, y)$ выведите отношения главной и побочной кривизны $\frac{\alpha}{\beta}$ в точке максимума. Будем считать, что если $\frac{\alpha}{\beta} > r_0 = 10$ , то это граница, и эту точку брать не будем. При реализации функции не вычисляйте напрямую $\alpha$ и $\beta$ .

def filter_edges(
    dog_level: np.ndarray,
    kps: list[Keypoint],
    r_0: float = 10.0
) -> list[Keypoint]:
    # YOUR CODE HERE
    raise NotImplementedError()

Вычисление характеристик признаков инвариантных к повороту¶

Теперь, после того, как мы вычислили все признаки инвариантные к размеру и обработали их, пришло время заняться поворотом.

В этом мы будем опираться на градиенты - на то есть несколько причин, например, хорошее фиксирование локальных особонностей, при небольшом изменении освещения градиент домножается на константу, в остальном не меняется. Есть и более формальные объяснения, которые рассмотрены не будут.

Для того, чтобы определить “ориентацию” точки, рассмотрим значения градиента в какой-то её окрестности, и присвоим им веса с помощью Гауссова распределения. В окрестность будут входить точки расположенные на манхэттенском расстоянии не более $1.5 \sigma_{or}$ , где $\sigma_or = 3\sigma_{kp}$ . Таким образом, чем дальше точка, тем меньше она будет вносить вклад в результат. Для каждой точки $p = (x, y)^T$ из окрестности вес будет $\omega(p) = \exp(- \frac{||p - p_0||_2^2}{2 \sigma_{or}^2})$ .

Далее, для каждой точки вычисляется угол и модуль её градиента, и добавляется в гистограмму с ранее вычисленным весом. Однако, у такого подхода есть небольшая проблема - точки близкие к граничным углам при малых поворотах могут существенно изменять вид диаграммы (они “перепыгивают” в другой промежуток). Поэтому, чтобы это исправить, каждая точка вносит линейный вклад в 2 ячейки. Поясним на примере.

Пусть есть точка с взвешенным модулем $m$ и углом 0.19. Так же, пусть границы столбцов гистограммы - углы $0, 0.1, 0.2, \dots$ . Очевидно, что эта точка намного ближе к 0.2, чем к 0.1, но без модификаций её модуль уйдет польностью в столбец 0.1. Поэтому, вычисляется относительная близость к 0.1: $\frac{0.19 - 0.1}{0.1} = 0.9$ , и к столбцу 0.1 прибавляется $(1-0.9)m$ , а к столбцу 0.2 – $0.9 m$ . Таким образом, гистограмма получается намного устойчивее. Так же, можно усреднить столбцы с соседними (циклическая свертка с константным фильтром длины 3), таким образом, какие-то выбросы намного реже будут глобальным максимумом на гистограмме.

Теперь из полученной гистограммы необходимо посчитать число, которое будет считаться “ориентацией” точки. Существует большое количество способов это делать, но самый простой - просто взять максимум. В нашей реализации мы пойдем немного дальше - мы будем брать не только глобальные, но и локальные (с соседями) максимумы, если они не меньше 0.8 от глобального. Таким образом, при большом количестве изменений вокруг точки не получится случайно выбрать похожие направления для точек отвечающих за разные места на картинке - даже при совпадении глобальных максимумов, по локальным будет понятно, что это разные объекты. Так же, можно уточнять истинное положение максимума делая квадратичную аппроксимацию по столбцу и его соседям - похоже, как мы делали выше.

Задача 22 (1 балл)

Вычислите истинное значение угла для максимума используя квадратичную аппроксимацию.

Решение:

Реализуйте алгоритм в функции calculate_orientations. Если для какой-то точки получится больше одной ориентации - просто записывайте в oriented её дубликаты с разными ориентациями.

def calculate_orientations(
    gauss_pyr: list[list[np.ndarray]],
    kps: list[Keypoint],
) -> list[Keypoint]:
    oriented: list[Keypoint] = []
    n_bins = 36 # количество столбцов в гистограмме
    # YOUR CODE HERE
    raise NotImplementedError()
    return oriented

Кодирование признаков¶

Осталось сделать последний шаг - на основе координат признаков и их ориентации построить “отпечаток”, чтобы эти признаки можно было сравнивать с признаками других картинок. Для этого опять обратимся к взвешиванию градиентов и гистограмм.

Идея следующая: возьмем для того гауссиана 16 ( $4\times4$ ) квадратов так, чтобы координаты признака находились по центру, каждый квадрат со стороной $3\sigma_{kp}$ . Точно так же взвесим их в зависимости от расстояния с $\sigma = 2 \cdot 3\sigma_{kp}$ чтобы точки ближе к признаку оказывали большее влияние. После этого, в каждом квадрате построим гистограммы с направлениями вектора градиентов, как раньше. Но, в отличии от вычислений ориентации, тут уже не 1, а 16 гистограмм, поэтому помимо соседних ячеек, каждую точку надо линейно распределять между ближайшим квадратом по $x$ и $y$ (если они конечно существуют). Например, если рассматривается точка в середине одного из квадратов, то она не дает вклада в соседние гистограммы, а если она находится на границе - вклад будет равным ( $0.5\omega m$ для каждой гистограммы).

Таким образом, при небольших сдвигах и поворотах признака полученные 16 гистограмм будут меняться слабо. Теперь осталось их записать в вектор, и отнормировать, затем приравнять все компоненты больше 0.2 к 0.2, и отнормировать ещё раз - таким образом, те объекты, что создают большой по модулю градиент направленный в одну сторону (например, прямые линии) в нескольких ячейках не будут мешать сравнивать картинку в целом.

Реализуйте алгоритм вычисления кодирующего вектора для одной точки, используя размытую фотографию нужного масштаба в функции calculate_kp_descriptor, и вычисление векторов для всех точек в функции compute_descriptors, используя предпосчитанные картинки всех масштабов с размытием.

def calculate_kp_descriptor(gauss_blurred: np.ndarray, kp: Keypoint) -> np.ndarray:
    # YOUR CODE HERE
    raise NotImplementedError()

def compute_descriptors(gauss_pyr: list[list[np.ndarray]], kps: list[Keypoint]) -> np.ndarray:
    descs = []
    # YOUR CODE HERE
    raise NotImplementedError()
    return np.stack(descs, axis=0).astype(np.float32)

Итоговый алгоритм и результаты работы¶

Теперь у нас есть всё, чтобы сделать SIFT. Напишите функию SIFT, которая вычисляет список признаков с ориентациями, и векторы их кодирующие.

# params example
# params = {
#     'octaves': 12,
#     'S': 3,
#     'sigma0': 1.6,
#     'sigma_in': 0.5,
#     'pad': 'mirror',
# }


def SIFT(img_gray: np.ndarray, params: dict, ) -> Tuple[list[Keypoint], np.ndarray]:
    # YOUR CODE HERE
    raise NotImplementedError()

Задача 23 (11 баллов)

Возспользуйтесь SIFT и заранее написанными функциями чтобы проиллюстрировать, как на двух фото одного и того же места сопоставляются точки.

img1 = cv2.imread("maps_panorama/image1.png", cv2.IMREAD_COLOR)
img2 = cv2.imread("maps_panorama/image2.png", cv2.IMREAD_COLOR)
img1 = cv2.cvtColor(img1, cv2.COLOR_BGR2RGB)
img2 = cv2.cvtColor(img2, cv2.COLOR_BGR2RGB)

params = {
        'octaves': 12,
        'S': 3,
        'sigma0': 1.6,
        'sigma_in': 0.5,
        'pad': 'mirror',
    }
kps1, d1 = SIFT(to_gray_float32(img1), params)
kps2, d2 = SIFT(to_gray_float32(img2), params)

matches = match_descriptors(d1, d2, ratio=0.8)
print(f"Matches after ratio test: {len(matches)}")
show_matches(to_gray_float32(img1), kps1, to_gray_float32(img2), kps2, matches, max_show=200)

---------------------------------------------------------------------------
error                                     Traceback (most recent call last)
Cell In[117], line 3
      1 img1 = cv2.imread("maps_panorama/image1.png", cv2.IMREAD_COLOR)
      2 img2 = cv2.imread("maps_panorama/image2.png", cv2.IMREAD_COLOR)
----> 3 img1 = cv2.cvtColor(img1, cv2.COLOR_BGR2RGB)
      4 img2 = cv2.cvtColor(img2, cv2.COLOR_BGR2RGB)
      6 params = {
      7         'octaves': 12,
      8         'S': 3,
   (...)
     11         'pad': 'mirror',
     12     }

error: OpenCV(4.10.0) D:\a\opencv-python\opencv-python\opencv\modules\imgproc\src\color.cpp:196: error: (-215:Assertion failed) !_src.empty() in function 'cv::cvtColor'

from lab_utils import assemble_and_show_all_collages
from pathlib import Path

p = Path('mars/')
imgs = []
for img in p.iterdir():
    im = cv2.imread(img, cv2.IMREAD_COLOR)
    im = cv2.cvtColor(im, cv2.COLOR_BGR2RGB)
    imgs.append(im)
print(f'len(imgs)={len(imgs)}')
results = assemble_and_show_all_collages(
    imgs,
    SIFT,
    ransac_thresh=3.0,
    min_matches_to_link=11,
    blend_sigma=0.0,
    max_cols=2
)
# Каждая запись results[k] содержит:
# 'panorama': np.ndarray[H,W,3] float32 в [0,1]
# 'placed_indices': индексы исходных картинок, попавших в этот коллаж
# 'failed_indices': индексы картинок из компоненты, которые не удалось надёжно пристыковать
# 'transforms': словарь {idx -> H_ref<-idx}

Homeworks

IMDE, Homework-2, Placement Optimization in Circuit Design